【壓縮機網】七、夾角γ為90°即所謂的倒“T”型機器的計算
7.1用基礎理論分析圖13形式順時針轉動時慣性力
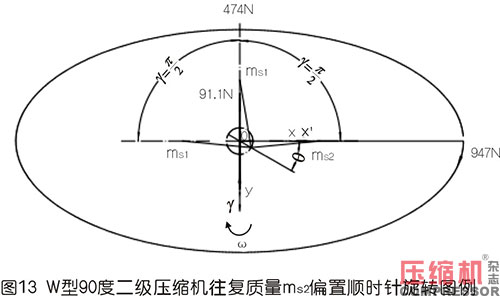
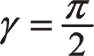
①一階慣性力的計算
由于90°采用三角函數計算相比較復數運算更簡單一些,以下全部采用三角函數法直接計算,以下兩個方向合力的構成都按圖示依次寫出。
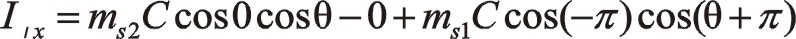
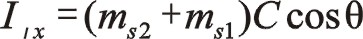
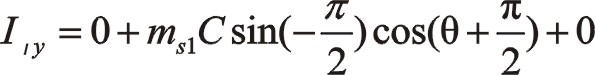
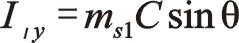
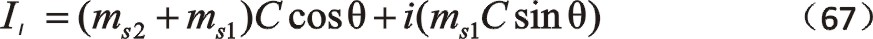
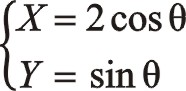
坐標系如圖所示順轉0°后,變成了氣缸對稱分布的主方向。這時的轉換矩陣為 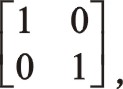
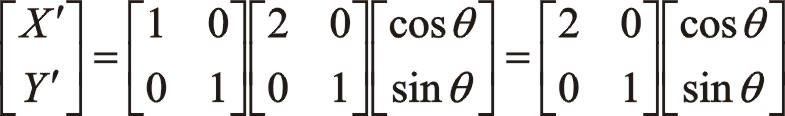

②二階慣性力的計算
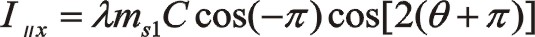
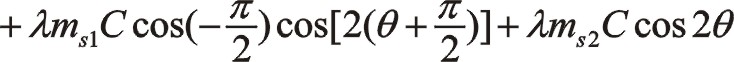
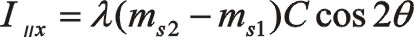
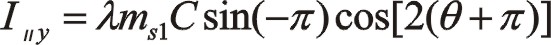
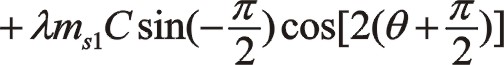
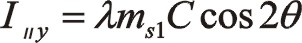

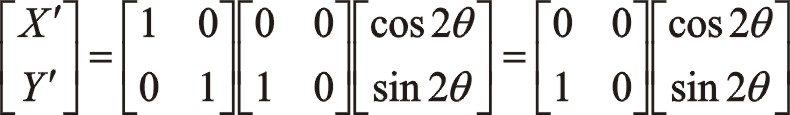

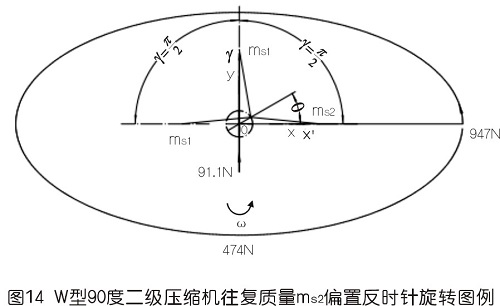
7.2用基礎理論分析圖14形式反時針轉動時慣性力
①一階慣性力的計算
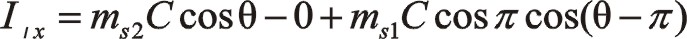
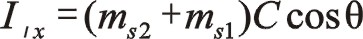
反轉時實部值可將順轉的實部值中“θ”換為“-θ”,因是余弦函數所以等于其自身。
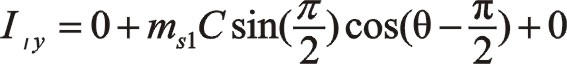
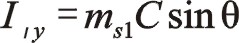
同樣,反轉時虛部值可將順轉的實部值中“θ”換為“-θ”,再加一個“-”,所以經該運算后還等于其自身。
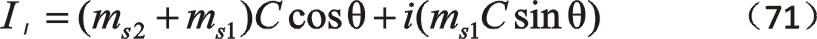
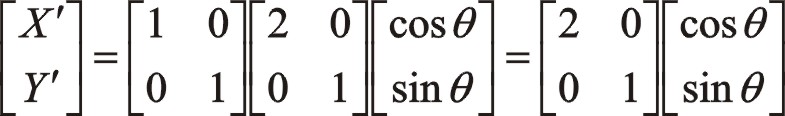

②二階慣性力的計算
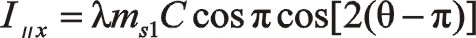
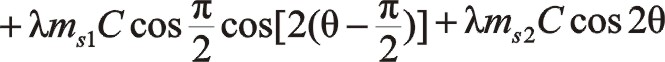
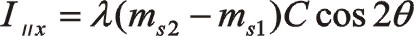
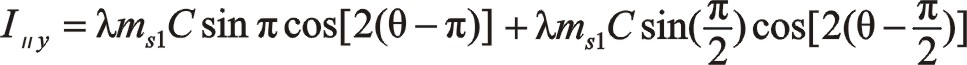
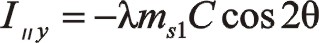

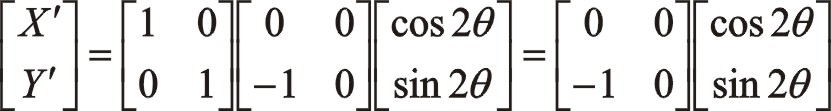

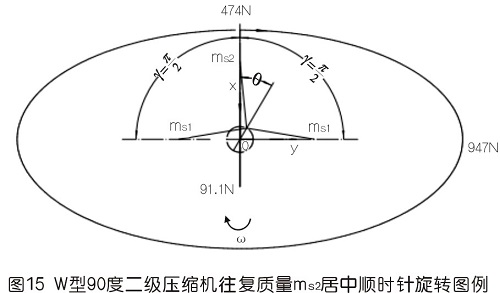
7.3用基礎理論分析圖15形式順時針轉動時慣性力
①一階慣性力的計算
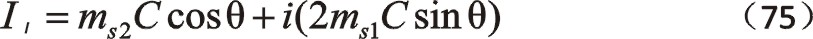
若兩質量相等,則可以得出W型90°壓縮機上述三種情形一階慣性力的橢圓的短長軸之比為0.5。
②二階慣性力的計算

根據式(76),若兩質量相等,可得出W型90°壓縮機上述三種情形二階慣性力是一段直線,關于原點對稱。
7.4總結
本處以安徽華晶機械有限公司生產的WW-0.9/10B-Q型全無油二級空壓機為模版,假定氣缸夾角為90°,計算其一、二階往復慣性力。此處先假定三列往復質量相等,即ms為1.8kg,曲柄半徑為0.0375m,曲柄半徑連桿比λ為37.5/195,角速度ω為2π×(800/60)rad/s,現將上述結構參數分別代入上文中所列的相關公式中,運用計算機內EXCEL程序列表、繪圖計算分析,計算的結果繪制在圖13、圖14、圖15中,可以得到以下結論:
1)一階慣性力由60°分布的圓變成橢圓,且橢圓的短長軸之比由1變成0.5,平均值由711N變成731N,有所增大;方向由跟隨變成近似跟隨。上面三圖中已畫出一、二階慣性力剛開始時的矢量線,用橢圓斷開表示。
2)二階慣性力說明,其橢圓短長軸之比由0.333變成不是橢圓是直線。力的平均值由96.9N變成57.9N,有所減小。方向初看是亂的,但很有規律,因為三角函數是周期函數。這個規律待人們去認識、研究、發現,找尋合適的機構來平衡。
7.5一致性方程
由于前面已經介紹了由中間列推導出偏置列的一致性方程,其實也能夠在三列往復質量相等的情況下,由左偏列推導出右偏列的一致性方程。現以γ為90°時為例,對其一階力寫出左右偏置之間的一致性方程,它涉及圖13、圖14的關系,其矩陣轉換方程如下:
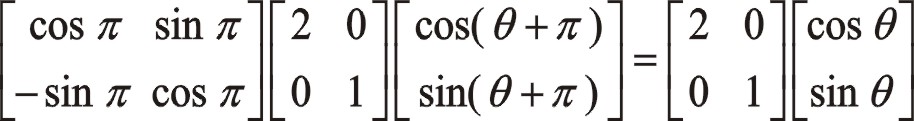
經矩陣運算,方程成立。二階力請讀者自己寫出。
八、結束語
8.1所有公式的換位型式
當將圖1中的坐標系建立在氣缸分布的中心對稱位置時,即x軸向上,y軸向右時,也就是超前60°,都有它們的換位公式。例如,式(9)的,
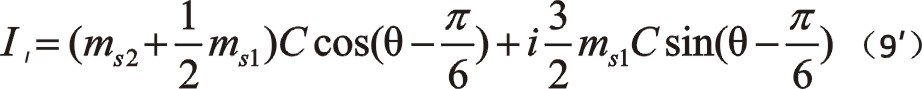
例如,式(24)的,
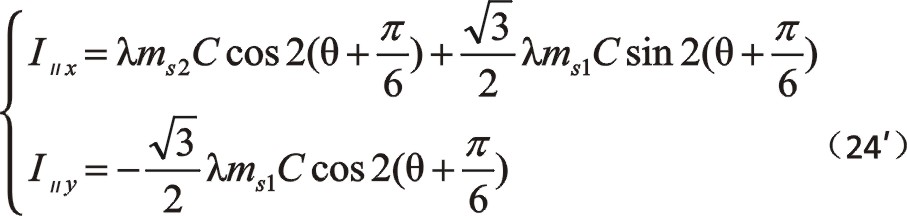
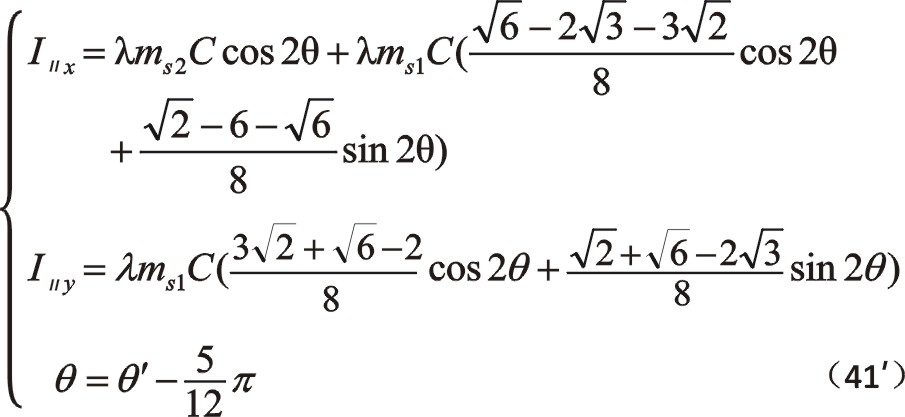
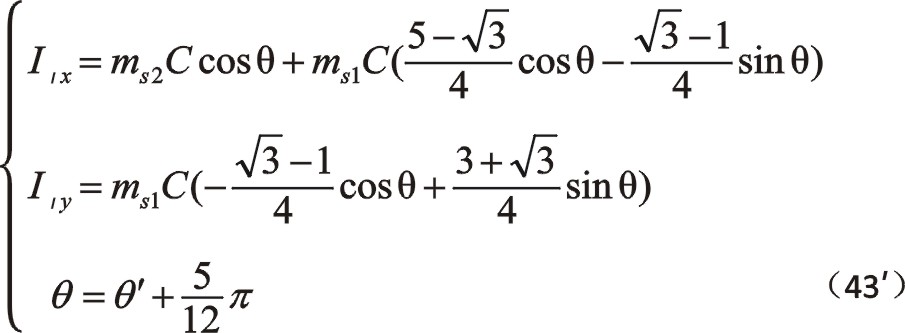
余不列舉。換位公式結合計算機來顯示分析,可以方便地看出ms2≠ms1時慣性力圖形的偏轉歧化現象。ms2增大,一階慣性力曲線就向該方向增長,數值越大增長越多。
8.2三列往復質量相等時慣性力簡圖
下面給出上文中當ms1=ms2=m時,令 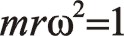 ,
,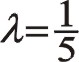 ,四種情形下慣性力的大小與簡易圖像,一、二階慣性力矢徑點的旋轉方向都是等同于曲柄旋轉方向,用于設計平衡裝置時所先行的理論。
,四種情形下慣性力的大小與簡易圖像,一、二階慣性力矢徑點的旋轉方向都是等同于曲柄旋轉方向,用于設計平衡裝置時所先行的理論。

8.3展望
①夾角為其它角度諸如30°和120°等時不展開討論其公式了,但都可以寫出它們通用的代數式。對于W型列間夾角為γ、三列往復質量相等時,其慣性力的參數方程如下,從氣缸分布的主方向位置算起。要注意的是文中的理論僅適用于單曲拐的角度式壓縮機,對于多曲拐的或者一個直軸上套三個不同相位偏心塊機構,該理論都不適用,對于單曲拐角度式蚌線機構適用。為了更清楚地弄明白單曲拐W型壓縮機,甚至全圓周范圍內星型式角度式壓縮機運轉時往復慣性力特性構成,這里很有必要推導出其通用的一、二階往復慣性力表達式,諸如圖3中所示的往復質量分布的型式,有
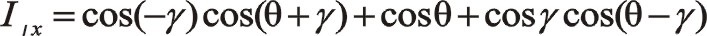
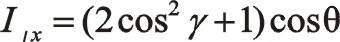
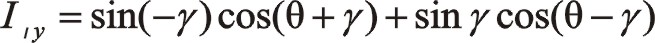
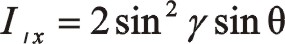

式(77)是一階往復慣性力參數方程表達式。
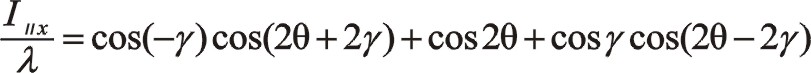
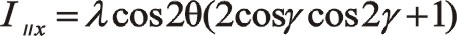
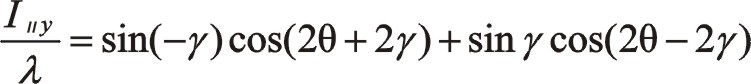

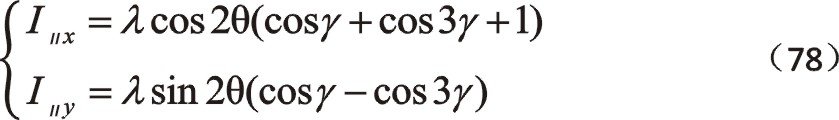
式(78)是二階往復慣性力參數方程表達式。
對于γ為120°的時候,就是三星型壓縮機,可以得出一、二階都是圓的分布。可是二階力卻是逆著曲柄方向旋轉,這種變化規律詭異多端,或許是一種橋梁,因為單曲拐的W型壓縮機都是一、二階慣性力旋轉方向與曲柄旋轉方向相同,如果角度超出W型結構,二階力開始變換方向,這與多曲拐的一些特性開始銜接。三星型壓縮機,作者在2009年就發現了該變化規律,并且發表在相關文獻上,就是文末的參考文獻3。
經過大量地計算、研究、論證等表明:單曲拐的各種夾角γ的W結構的壓縮機機器,是以60°為分界線的,小于60°的一階慣性力圖的橢圓向豎直方向增長;等于60°的是標準圓;大于60°的則是向水平方向增長。總的來說,一階慣性力曲線是橢圓,包含有60°時為圓。由于壓縮機運轉時角速度為定值,根據開普勒第二定律,我們可以得到慣性力圖形上矢徑點運動速率大小的規律,也就是“在相等的時間內,行星與太陽的連線所掃過的面積相等。”通俗地說,通過距離中心近的點速率較快,而在橢圓長軸處的點通過較慢。這也是網絡知乎上某些人談論的所謂的“橢圓向(半)徑的旋轉”的問題,說的是高速行駛的汽車的車輪,帶有輪輞的,如果我們從側面一個角度看該車輪,這就涉及到橢圓向徑的旋轉,側看圓形的車輪即是橢圓形的,這也是投影視角給人們造成的現象。在橢圓的前后位置,也是橢圓短軸方向上速度較快,而在上下位置,即是橢圓長軸方向速度較慢,實際上行駛的車輪時勻速圓周運動,車輪上的所有點移動速度相同。這里與慣性力曲線上的點移動速度的變化相類似,遵循開普勒面積定理,從圖線上點的移動速度變化率來看,近的地方移動速率快,而遠的地方移動速率慢。二階慣性力基本上都是橢圓,也包括直線,讀者可以通過圖16了解其大小,其運動的速率也符合開普勒第二定律。
②對于W型三列往復質量都不相等時,可有什么公式用于計算?文中的公式(7)、(11)等適用。對于式(15)、式(32),因ms2不同于ms1時,所引起橢圓的偏轉和幅值相位變化,可有什么理論公式說明該問題,歡迎讀者們進行討論交流。網絡百度上某人曾給出關于橢圓旋轉引起幅值變化的矩陣代數式,見下。不知這個方程對解決這個問題可有幫助。
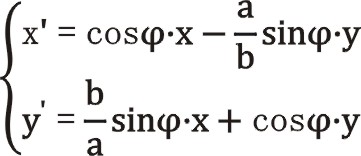
對于以上文章羅列的四種角度,因有兩種往復運動質量,因有ms2列處于偏置和居中兩種情形,我們要對一階慣性力圖有明確的認識,總結如下:ms2列處于居中分布時,不會引起橢圓的偏轉,即橢圓長短軸位置不變而其長短軸大小發生變化。例如75°時由式(50),當ms2= 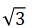 ms1時;45°和90°時依式(65)、(75);當ms2=0時,有前兩項能實現一階慣性力成圓路徑變化,這在工業上都有它的應用:例如45°時若二級往復質量為0,就變成V型90°的壓縮機機器;90°時若二級往復質量為0,就變成單曲拐兩列對置式壓縮機機器,其一階慣性力成一段直線,需要用專門的機構來平衡它。這不同于西安交通大學教材上講到的曲軸為均布三曲拐、外部的三個氣缸在水平方向呈對置式分布的機器。不過這些都要考慮到二階慣性力是否達到最小,要評估決定一下二階慣性力是否采用專門的機構來平衡它,或者因較小就任其存在。對于ms2列偏置的情況,若ms2≠ms1,一般都會引起一階慣性力圖像歧化現象,即橢圓圖像的偏轉(不是上面介紹的“橢圓半徑的旋轉”的概念)和幅值相位的變化。例如對式(32)若ms2列增大則一階慣性力橢圓微微地向ms2列偏轉;而對于60°時由式(9),則不是這種情況類似出現,因為60°占據了分界線的位置。ms2列增大則在與主對稱位置成30°的方向,也就是ms2列活塞方向增長成橢圓變化,不是微微地由水平方向偏轉而是在這個方向上增長。對45°、90°的讀者自行分析。
ms1時;45°和90°時依式(65)、(75);當ms2=0時,有前兩項能實現一階慣性力成圓路徑變化,這在工業上都有它的應用:例如45°時若二級往復質量為0,就變成V型90°的壓縮機機器;90°時若二級往復質量為0,就變成單曲拐兩列對置式壓縮機機器,其一階慣性力成一段直線,需要用專門的機構來平衡它。這不同于西安交通大學教材上講到的曲軸為均布三曲拐、外部的三個氣缸在水平方向呈對置式分布的機器。不過這些都要考慮到二階慣性力是否達到最小,要評估決定一下二階慣性力是否采用專門的機構來平衡它,或者因較小就任其存在。對于ms2列偏置的情況,若ms2≠ms1,一般都會引起一階慣性力圖像歧化現象,即橢圓圖像的偏轉(不是上面介紹的“橢圓半徑的旋轉”的概念)和幅值相位的變化。例如對式(32)若ms2列增大則一階慣性力橢圓微微地向ms2列偏轉;而對于60°時由式(9),則不是這種情況類似出現,因為60°占據了分界線的位置。ms2列增大則在與主對稱位置成30°的方向,也就是ms2列活塞方向增長成橢圓變化,不是微微地由水平方向偏轉而是在這個方向上增長。對45°、90°的讀者自行分析。
上面介紹的四種情形,對于單曲拐式曲軸,所引起的一、二階慣性力圖線的旋轉方向均等同于曲柄旋轉方向,對較高等級的讀者來說,他們一定會明白一、二階往復慣性力不同視角下力矢的初始位置、運動方向、幅值變化大小、頻率。了解其公式、圖像等特征,則對其運轉時的變化規律特征成竹在胸、洞若觀火。
③文中的理論用于指導慣性力平衡機構設計,不光給出了總體圖像,還討論了實時的相位變化。例如圖6、圖9、圖12、圖15中兩種慣性力線斷開位置表示該型式的起始點位置,有助于指導平衡裝置初始位置的安裝,文獻4就給出了一種平衡裝置。
④依照作者目前所掌握的信息情況來說:V型60°的船用壓縮機,兩列的往復質量嚴格相等,采用正反轉平衡系統平衡了機器的一、二階往復慣性力。總的結構是在主軸的后端設置一個驅動齒輪,在水平線上左右設置一個二級齒輪,一個一級齒輪,共計五個齒輪。二級齒輪是驅動齒輪和一級齒輪的一半大。因為按照上面的計算方法或目前其他作者的文獻,可以得出:其一階慣性力是1:3的橢圓,二階慣性力是圓,采用左右兩個一級齒輪是將該該橢圓壓擴成圓,這兩個齒輪是反轉方向,一階慣性力最終在曲軸砣的最底部位置來平衡;兩個二級齒輪轉速高且與曲軸轉向同向,也是正轉方向,故名正反轉平衡系統。四個齒輪的軸線沿著主軸上都設置兩個軸承來支承,中間設置偏心塊形成離心力來平衡機器慣性力,左右設置的平衡箱讓旋轉系統在一個密閉的系統中工作。這種設計的結構總的指導思想是:慣性力實時作用在曲軸箱箱體中心線,離心旋轉的偏心塊的離心力也作用在曲軸箱體表面上,最終所有的外在力在曲軸箱表面上實現實時抵消。它的缺點是使曲軸箱體更復雜,平衡箱體內需設置更多的軸承。關于它設計時的旋轉質量的質徑積大小分配和初始安裝位置,請讀者自行分析。因此對于W型60°機器的二階慣性力,其特征也是短長軸為1:3的橢圓,它的平衡也可以采用這種思路來平衡。這都是外嚙合正反轉平衡技術的應用。
根據這個思路,對于W型75°等機器,也可以采用這種方法來平衡。不過所設計的平衡系統更復雜,理論上也能夠實現一、二階往復慣性力的完全平衡,這就是行星齒輪機構,包含有內、外嚙合正反轉平衡系統。V型機器也能夠應用行星齒輪機構來平衡其運轉時的慣性力。對于這些更高級的平衡措施,有需要時可以實行共同開發。這些都是建立在三列往復質量要求完全相等的情況下,對比分析也可以得出60°機器是W型壓縮機的優選角度。
⑤對于180°雙拐W型壓縮機,若對一、二階往復慣性力不采用平衡措施,由于雙拐之間的距離不可忽略,雖然總的一、二階往復慣性力矢量大小能夠實現瞬時抵消,但由于力的作用點不同,在機器內部瞬時形成了周期性的往復一、二階慣性力矩,最終作用在機器兩端的主軸承上,這要引起人們注意。
8.4如何做好壓縮機事業與產品
①加強基礎研究,推動原始創新
文中的理論派生出W型壓縮機各種型式,有助于人們開發異于60°的壓縮機。壓縮機的結構形式也會形成“百花齊放、百家爭鳴”的局面。
②結合理論迫切需要解決現實存在的各種問題
我國無油壓縮機的發展,從50年代起步,經歷了二十多年火熱發展期,在2010年左右進入飽和期,因螺桿機發展限制了活塞機的發展。作者親眼目睹了中國大地上一些企業主經常抱怨:他的七、八百轉空壓機試機時一旦開起來,滿地跑,橫著拱,豎著挪,碰到一個地面的高點時又順便拐了一個彎,攔都攔不住。這是非常糟糕的現象,是機器的軸系動平衡設計工作沒有做好。動平衡中的待平衡的質量,包括旋轉質量和打個折后的往復質量,如果沒有弄明白其中的竅門,不一點一滴地摳出其中質心處質量,不明白往復質量如何打折,不懂得連桿質量如何分成,那開起來不跑才怪了。技術人要做的細活兒就是設法使空間旋轉剛體的質心落在主軸線上,這個工作做好了,就能減小機器的宏觀振動,并且還有能力來提高機器的轉速,提高機器的效率——機器的比質量,比體積指標也會大有改觀。當下的螺桿機為什么優秀?就是因為其轉速有二、三千轉。所以說,活塞機要想發展,就得重新作動平衡的優化設計,提高轉速,牽一發而動全身。同時講究往復質量的相等,以降低各缸蓋處測量點的振動烈度,振動問題好了,噪聲性能也會提上去一個等級。
溫馨提示:更多內容筆者將在關于三曲拐W型壓縮機的論文中探討。
<本文連載完!>
參考文獻
(1)宋瑞林,氣缸夾角為60°的V6車用發動機往復慣性力的平衡分析,[J],汽車技術,1988.8
(2)李松虎,3W型活塞壓縮機往復慣性力的分析,[J],壓縮機技術,1987.3
(3)陸鵬程,張光勝,三星型壓縮機振動問題研究,[J],安徽工程科技學院學報,2009.1
(4)王再順,夾角為90°的V型壓縮機往復慣性力平衡的探討,[J],壓縮機技術,1986.2
作者簡介
陸鵬程,男,安徽桐城人,海軍工程大學在職碩士畢業。現在中國人民解放軍第四八一二工廠,安徽華晶機械有限公司工作,高級工程師。研究方向:壓縮機研究與強度設計。
【壓縮機網】七、夾角γ為90°即所謂的倒“T”型機器的計算
7.1用基礎理論分析圖13形式順時針轉動時慣性力

![]()
①一階慣性力的計算
由于90°采用三角函數計算相比較復數運算更簡單一些,以下全部采用三角函數法直接計算,以下兩個方向合力的構成都按圖示依次寫出。
![]()
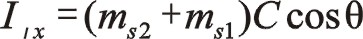
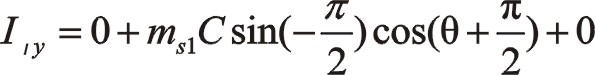
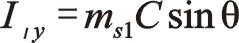
![]()
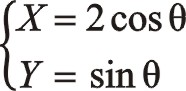
坐標系如圖所示順轉0°后,變成了氣缸對稱分布的主方向。這時的轉換矩陣為 ![]()
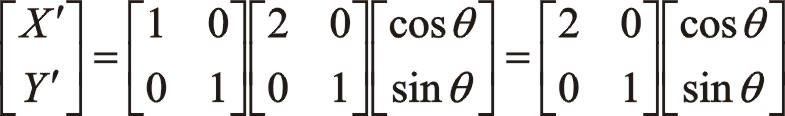

②二階慣性力的計算
![]()
![]()
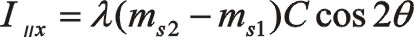
![]()
![]()
![]()

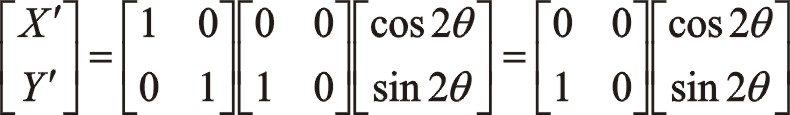

7.2用基礎理論分析圖14形式反時針轉動時慣性力

①一階慣性力的計算
![]()
![]()
反轉時實部值可將順轉的實部值中“θ”換為“-θ”,因是余弦函數所以等于其自身。
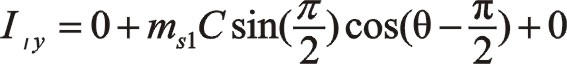
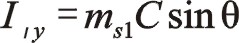
同樣,反轉時虛部值可將順轉的實部值中“θ”換為“-θ”,再加一個“-”,所以經該運算后還等于其自身。
![]()
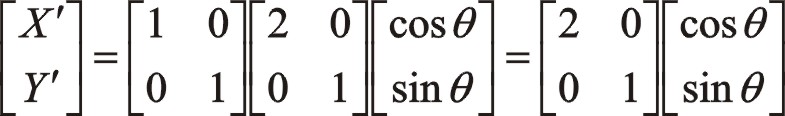

②二階慣性力的計算
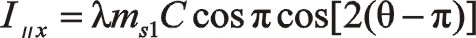
![]()
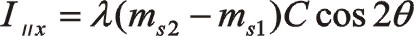
![]()
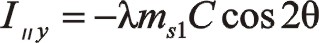

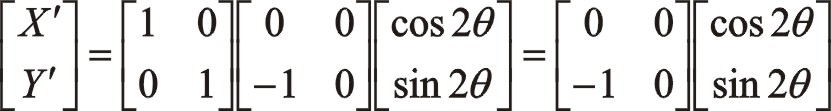

7.3用基礎理論分析圖15形式順時針轉動時慣性力

①一階慣性力的計算
![]()
若兩質量相等,則可以得出W型90°壓縮機上述三種情形一階慣性力的橢圓的短長軸之比為0.5。
②二階慣性力的計算

根據式(76),若兩質量相等,可得出W型90°壓縮機上述三種情形二階慣性力是一段直線,關于原點對稱。
7.4總結
本處以安徽華晶機械有限公司生產的WW-0.9/10B-Q型全無油二級空壓機為模版,假定氣缸夾角為90°,計算其一、二階往復慣性力。此處先假定三列往復質量相等,即ms為1.8kg,曲柄半徑為0.0375m,曲柄半徑連桿比λ為37.5/195,角速度ω為2π×(800/60)rad/s,現將上述結構參數分別代入上文中所列的相關公式中,運用計算機內EXCEL程序列表、繪圖計算分析,計算的結果繪制在圖13、圖14、圖15中,可以得到以下結論:
1)一階慣性力由60°分布的圓變成橢圓,且橢圓的短長軸之比由1變成0.5,平均值由711N變成731N,有所增大;方向由跟隨變成近似跟隨。上面三圖中已畫出一、二階慣性力剛開始時的矢量線,用橢圓斷開表示。
2)二階慣性力說明,其橢圓短長軸之比由0.333變成不是橢圓是直線。力的平均值由96.9N變成57.9N,有所減小。方向初看是亂的,但很有規律,因為三角函數是周期函數。這個規律待人們去認識、研究、發現,找尋合適的機構來平衡。
7.5一致性方程
由于前面已經介紹了由中間列推導出偏置列的一致性方程,其實也能夠在三列往復質量相等的情況下,由左偏列推導出右偏列的一致性方程。現以γ為90°時為例,對其一階力寫出左右偏置之間的一致性方程,它涉及圖13、圖14的關系,其矩陣轉換方程如下:
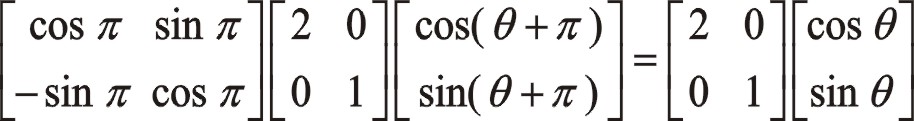
經矩陣運算,方程成立。二階力請讀者自己寫出。
八、結束語
8.1所有公式的換位型式
當將圖1中的坐標系建立在氣缸分布的中心對稱位置時,即x軸向上,y軸向右時,也就是超前60°,都有它們的換位公式。例如,式(9)的,
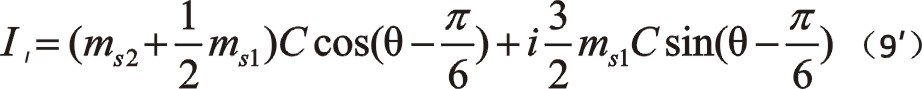
例如,式(24)的,
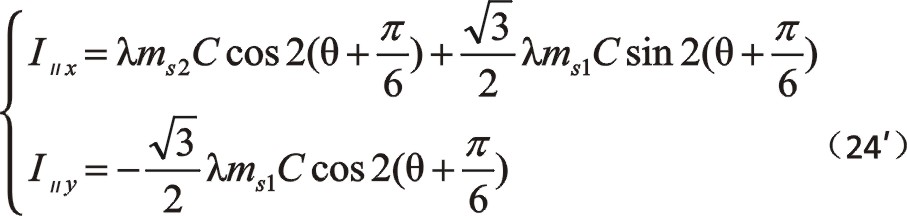
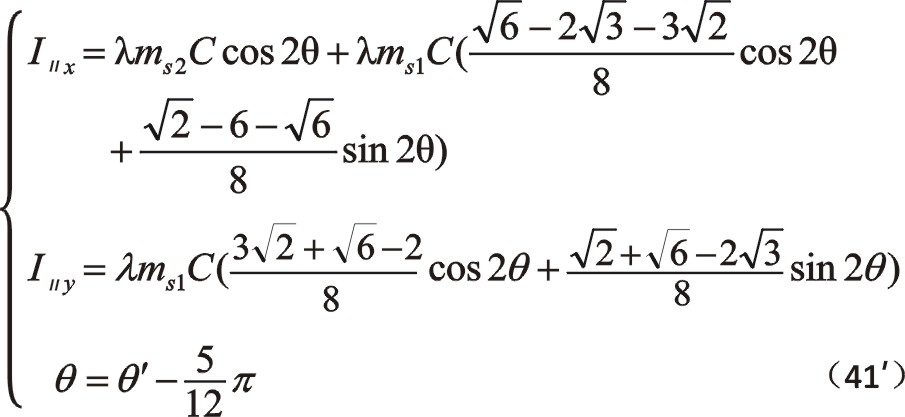
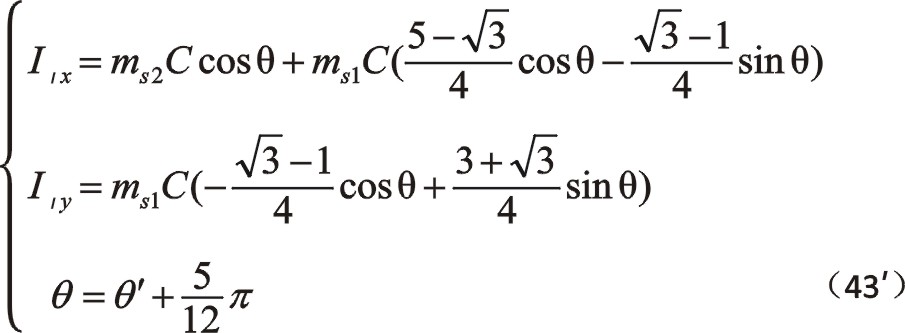
余不列舉。換位公式結合計算機來顯示分析,可以方便地看出ms2≠ms1時慣性力圖形的偏轉歧化現象。ms2增大,一階慣性力曲線就向該方向增長,數值越大增長越多。
8.2三列往復質量相等時慣性力簡圖
下面給出上文中當ms1=ms2=m時,令 ![]() ,
,![]() ,四種情形下慣性力的大小與簡易圖像,一、二階慣性力矢徑點的旋轉方向都是等同于曲柄旋轉方向,用于設計平衡裝置時所先行的理論。
,四種情形下慣性力的大小與簡易圖像,一、二階慣性力矢徑點的旋轉方向都是等同于曲柄旋轉方向,用于設計平衡裝置時所先行的理論。


8.3展望
①夾角為其它角度諸如30°和120°等時不展開討論其公式了,但都可以寫出它們通用的代數式。對于W型列間夾角為γ、三列往復質量相等時,其慣性力的參數方程如下,從氣缸分布的主方向位置算起。要注意的是文中的理論僅適用于單曲拐的角度式壓縮機,對于多曲拐的或者一個直軸上套三個不同相位偏心塊機構,該理論都不適用,對于單曲拐角度式蚌線機構適用。為了更清楚地弄明白單曲拐W型壓縮機,甚至全圓周范圍內星型式角度式壓縮機運轉時往復慣性力特性構成,這里很有必要推導出其通用的一、二階往復慣性力表達式,諸如圖3中所示的往復質量分布的型式,有
![]()
![]()
![]()
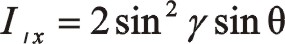

式(77)是一階往復慣性力參數方程表達式。
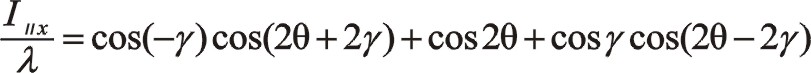
![]()
![]()
![]()
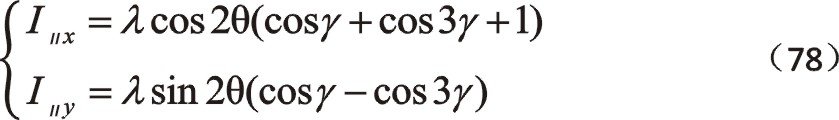
式(78)是二階往復慣性力參數方程表達式。
對于γ為120°的時候,就是三星型壓縮機,可以得出一、二階都是圓的分布。可是二階力卻是逆著曲柄方向旋轉,這種變化規律詭異多端,或許是一種橋梁,因為單曲拐的W型壓縮機都是一、二階慣性力旋轉方向與曲柄旋轉方向相同,如果角度超出W型結構,二階力開始變換方向,這與多曲拐的一些特性開始銜接。三星型壓縮機,作者在2009年就發現了該變化規律,并且發表在相關文獻上,就是文末的參考文獻3。
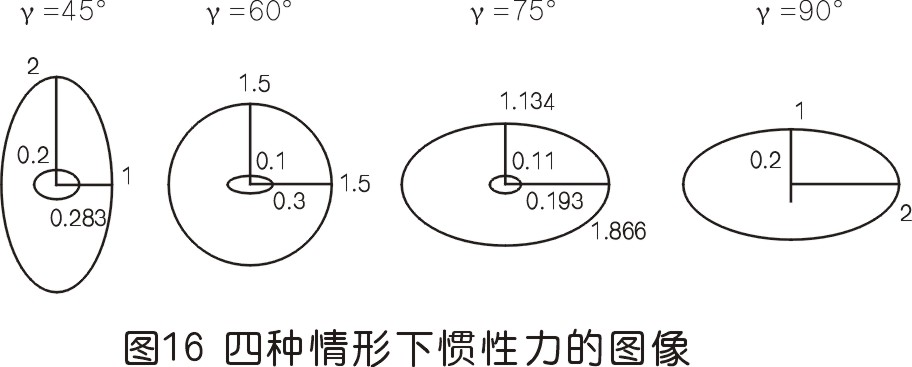
經過大量地計算、研究、論證等表明:單曲拐的各種夾角γ的W結構的壓縮機機器,是以60°為分界線的,小于60°的一階慣性力圖的橢圓向豎直方向增長;等于60°的是標準圓;大于60°的則是向水平方向增長。總的來說,一階慣性力曲線是橢圓,包含有60°時為圓。由于壓縮機運轉時角速度為定值,根據開普勒第二定律,我們可以得到慣性力圖形上矢徑點運動速率大小的規律,也就是“在相等的時間內,行星與太陽的連線所掃過的面積相等。”通俗地說,通過距離中心近的點速率較快,而在橢圓長軸處的點通過較慢。這也是網絡知乎上某些人談論的所謂的“橢圓向(半)徑的旋轉”的問題,說的是高速行駛的汽車的車輪,帶有輪輞的,如果我們從側面一個角度看該車輪,這就涉及到橢圓向徑的旋轉,側看圓形的車輪即是橢圓形的,這也是投影視角給人們造成的現象。在橢圓的前后位置,也是橢圓短軸方向上速度較快,而在上下位置,即是橢圓長軸方向速度較慢,實際上行駛的車輪時勻速圓周運動,車輪上的所有點移動速度相同。這里與慣性力曲線上的點移動速度的變化相類似,遵循開普勒面積定理,從圖線上點的移動速度變化率來看,近的地方移動速率快,而遠的地方移動速率慢。二階慣性力基本上都是橢圓,也包括直線,讀者可以通過圖16了解其大小,其運動的速率也符合開普勒第二定律。
②對于W型三列往復質量都不相等時,可有什么公式用于計算?文中的公式(7)、(11)等適用。對于式(15)、式(32),因ms2不同于ms1時,所引起橢圓的偏轉和幅值相位變化,可有什么理論公式說明該問題,歡迎讀者們進行討論交流。網絡百度上某人曾給出關于橢圓旋轉引起幅值變化的矩陣代數式,見下。不知這個方程對解決這個問題可有幫助。
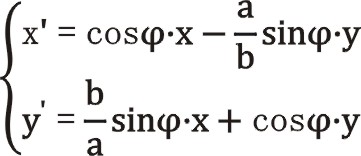
對于以上文章羅列的四種角度,因有兩種往復運動質量,因有ms2列處于偏置和居中兩種情形,我們要對一階慣性力圖有明確的認識,總結如下:ms2列處于居中分布時,不會引起橢圓的偏轉,即橢圓長短軸位置不變而其長短軸大小發生變化。例如75°時由式(50),當ms2= ![]() ms1時;45°和90°時依式(65)、(75);當ms2=0時,有前兩項能實現一階慣性力成圓路徑變化,這在工業上都有它的應用:例如45°時若二級往復質量為0,就變成V型90°的壓縮機機器;90°時若二級往復質量為0,就變成單曲拐兩列對置式壓縮機機器,其一階慣性力成一段直線,需要用專門的機構來平衡它。這不同于西安交通大學教材上講到的曲軸為均布三曲拐、外部的三個氣缸在水平方向呈對置式分布的機器。不過這些都要考慮到二階慣性力是否達到最小,要評估決定一下二階慣性力是否采用專門的機構來平衡它,或者因較小就任其存在。對于ms2列偏置的情況,若ms2≠ms1,一般都會引起一階慣性力圖像歧化現象,即橢圓圖像的偏轉(不是上面介紹的“橢圓半徑的旋轉”的概念)和幅值相位的變化。例如對式(32)若ms2列增大則一階慣性力橢圓微微地向ms2列偏轉;而對于60°時由式(9),則不是這種情況類似出現,因為60°占據了分界線的位置。ms2列增大則在與主對稱位置成30°的方向,也就是ms2列活塞方向增長成橢圓變化,不是微微地由水平方向偏轉而是在這個方向上增長。對45°、90°的讀者自行分析。
ms1時;45°和90°時依式(65)、(75);當ms2=0時,有前兩項能實現一階慣性力成圓路徑變化,這在工業上都有它的應用:例如45°時若二級往復質量為0,就變成V型90°的壓縮機機器;90°時若二級往復質量為0,就變成單曲拐兩列對置式壓縮機機器,其一階慣性力成一段直線,需要用專門的機構來平衡它。這不同于西安交通大學教材上講到的曲軸為均布三曲拐、外部的三個氣缸在水平方向呈對置式分布的機器。不過這些都要考慮到二階慣性力是否達到最小,要評估決定一下二階慣性力是否采用專門的機構來平衡它,或者因較小就任其存在。對于ms2列偏置的情況,若ms2≠ms1,一般都會引起一階慣性力圖像歧化現象,即橢圓圖像的偏轉(不是上面介紹的“橢圓半徑的旋轉”的概念)和幅值相位的變化。例如對式(32)若ms2列增大則一階慣性力橢圓微微地向ms2列偏轉;而對于60°時由式(9),則不是這種情況類似出現,因為60°占據了分界線的位置。ms2列增大則在與主對稱位置成30°的方向,也就是ms2列活塞方向增長成橢圓變化,不是微微地由水平方向偏轉而是在這個方向上增長。對45°、90°的讀者自行分析。
上面介紹的四種情形,對于單曲拐式曲軸,所引起的一、二階慣性力圖線的旋轉方向均等同于曲柄旋轉方向,對較高等級的讀者來說,他們一定會明白一、二階往復慣性力不同視角下力矢的初始位置、運動方向、幅值變化大小、頻率。了解其公式、圖像等特征,則對其運轉時的變化規律特征成竹在胸、洞若觀火。
③文中的理論用于指導慣性力平衡機構設計,不光給出了總體圖像,還討論了實時的相位變化。例如圖6、圖9、圖12、圖15中兩種慣性力線斷開位置表示該型式的起始點位置,有助于指導平衡裝置初始位置的安裝,文獻4就給出了一種平衡裝置。
④依照作者目前所掌握的信息情況來說:V型60°的船用壓縮機,兩列的往復質量嚴格相等,采用正反轉平衡系統平衡了機器的一、二階往復慣性力。總的結構是在主軸的后端設置一個驅動齒輪,在水平線上左右設置一個二級齒輪,一個一級齒輪,共計五個齒輪。二級齒輪是驅動齒輪和一級齒輪的一半大。因為按照上面的計算方法或目前其他作者的文獻,可以得出:其一階慣性力是1:3的橢圓,二階慣性力是圓,采用左右兩個一級齒輪是將該該橢圓壓擴成圓,這兩個齒輪是反轉方向,一階慣性力最終在曲軸砣的最底部位置來平衡;兩個二級齒輪轉速高且與曲軸轉向同向,也是正轉方向,故名正反轉平衡系統。四個齒輪的軸線沿著主軸上都設置兩個軸承來支承,中間設置偏心塊形成離心力來平衡機器慣性力,左右設置的平衡箱讓旋轉系統在一個密閉的系統中工作。這種設計的結構總的指導思想是:慣性力實時作用在曲軸箱箱體中心線,離心旋轉的偏心塊的離心力也作用在曲軸箱體表面上,最終所有的外在力在曲軸箱表面上實現實時抵消。它的缺點是使曲軸箱體更復雜,平衡箱體內需設置更多的軸承。關于它設計時的旋轉質量的質徑積大小分配和初始安裝位置,請讀者自行分析。因此對于W型60°機器的二階慣性力,其特征也是短長軸為1:3的橢圓,它的平衡也可以采用這種思路來平衡。這都是外嚙合正反轉平衡技術的應用。
根據這個思路,對于W型75°等機器,也可以采用這種方法來平衡。不過所設計的平衡系統更復雜,理論上也能夠實現一、二階往復慣性力的完全平衡,這就是行星齒輪機構,包含有內、外嚙合正反轉平衡系統。V型機器也能夠應用行星齒輪機構來平衡其運轉時的慣性力。對于這些更高級的平衡措施,有需要時可以實行共同開發。這些都是建立在三列往復質量要求完全相等的情況下,對比分析也可以得出60°機器是W型壓縮機的優選角度。
⑤對于180°雙拐W型壓縮機,若對一、二階往復慣性力不采用平衡措施,由于雙拐之間的距離不可忽略,雖然總的一、二階往復慣性力矢量大小能夠實現瞬時抵消,但由于力的作用點不同,在機器內部瞬時形成了周期性的往復一、二階慣性力矩,最終作用在機器兩端的主軸承上,這要引起人們注意。
8.4如何做好壓縮機事業與產品
①加強基礎研究,推動原始創新
文中的理論派生出W型壓縮機各種型式,有助于人們開發異于60°的壓縮機。壓縮機的結構形式也會形成“百花齊放、百家爭鳴”的局面。
②結合理論迫切需要解決現實存在的各種問題
我國無油壓縮機的發展,從50年代起步,經歷了二十多年火熱發展期,在2010年左右進入飽和期,因螺桿機發展限制了活塞機的發展。作者親眼目睹了中國大地上一些企業主經常抱怨:他的七、八百轉空壓機試機時一旦開起來,滿地跑,橫著拱,豎著挪,碰到一個地面的高點時又順便拐了一個彎,攔都攔不住。這是非常糟糕的現象,是機器的軸系動平衡設計工作沒有做好。動平衡中的待平衡的質量,包括旋轉質量和打個折后的往復質量,如果沒有弄明白其中的竅門,不一點一滴地摳出其中質心處質量,不明白往復質量如何打折,不懂得連桿質量如何分成,那開起來不跑才怪了。技術人要做的細活兒就是設法使空間旋轉剛體的質心落在主軸線上,這個工作做好了,就能減小機器的宏觀振動,并且還有能力來提高機器的轉速,提高機器的效率——機器的比質量,比體積指標也會大有改觀。當下的螺桿機為什么優秀?就是因為其轉速有二、三千轉。所以說,活塞機要想發展,就得重新作動平衡的優化設計,提高轉速,牽一發而動全身。同時講究往復質量的相等,以降低各缸蓋處測量點的振動烈度,振動問題好了,噪聲性能也會提上去一個等級。
溫馨提示:更多內容筆者將在關于三曲拐W型壓縮機的論文中探討。
<本文連載完!>
參考文獻
(1)宋瑞林,氣缸夾角為60°的V6車用發動機往復慣性力的平衡分析,[J],汽車技術,1988.8
(2)李松虎,3W型活塞壓縮機往復慣性力的分析,[J],壓縮機技術,1987.3
(3)陸鵬程,張光勝,三星型壓縮機振動問題研究,[J],安徽工程科技學院學報,2009.1
(4)王再順,夾角為90°的V型壓縮機往復慣性力平衡的探討,[J],壓縮機技術,1986.2
作者簡介
陸鵬程,男,安徽桐城人,海軍工程大學在職碩士畢業。現在中國人民解放軍第四八一二工廠,安徽華晶機械有限公司工作,高級工程師。研究方向:壓縮機研究與強度設計。





網友評論
條評論
最新評論