【壓縮機網】〈接上期——〉
六、夾角γ為45°的計算
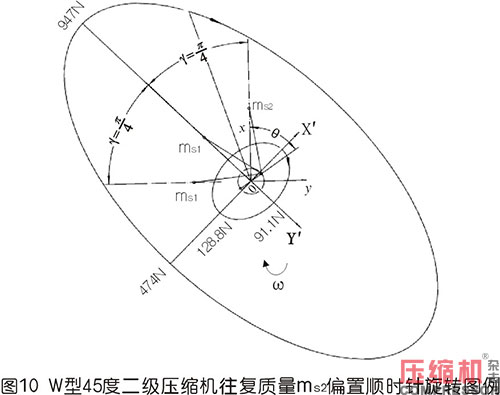
6.1用基礎理論分析圖10形式順時針轉動時慣性力
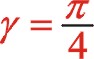
①一階慣性力的計算
一階慣性力用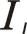 表示,下標
表示,下標 代表一階。按照圖10從左到右的閱讀順序,其一階慣性力合力的構成如(7)式所表達
代表一階。按照圖10從左到右的閱讀順序,其一階慣性力合力的構成如(7)式所表達
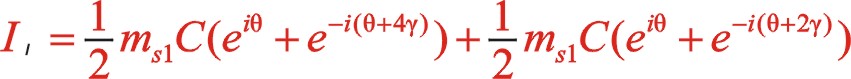

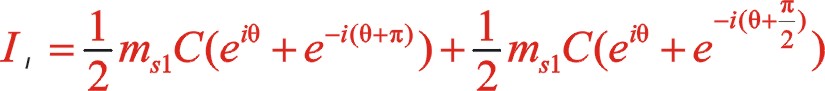
 、
、

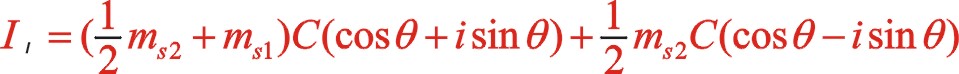


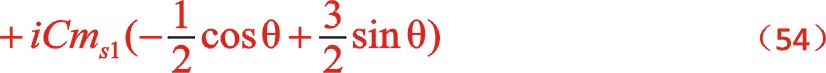

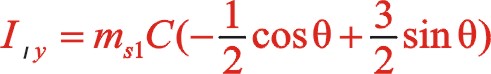
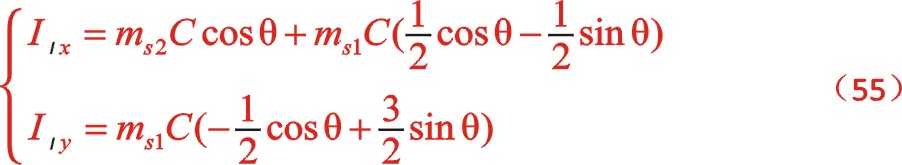


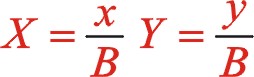

坐標系如圖所示順轉45°后,變成了氣缸對稱分布的主方向。一般的,根據坐標系的旋轉變換(不是坐標的旋轉變換,根據網絡百度上發布的信息仔細甄別:坐標的旋轉變換是指只有一個坐標系,有一個向量逆時針旋轉α后變成一個新的向量,新的點的坐標也可以采用矩陣運算來完成,而其矩陣運算的因子卻為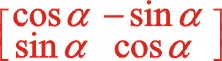 ,經矩陣的乘法運算后形成新的值還在原來的坐標系中度量,這一點與計算機圖學中作“X=X+1”賦值運算一樣。可以說坐標的旋轉變換與坐標系的旋轉變換是一對互為逆運算),有這樣的理論:對于標準的直角坐標系即x軸正方向向右,y軸的正方向向上,當xoy坐標系中x軸正方向向著y軸正方向轉動時為正值α時,也就是逆時針轉動,這時的轉換矩陣為
,經矩陣的乘法運算后形成新的值還在原來的坐標系中度量,這一點與計算機圖學中作“X=X+1”賦值運算一樣。可以說坐標的旋轉變換與坐標系的旋轉變換是一對互為逆運算),有這樣的理論:對于標準的直角坐標系即x軸正方向向右,y軸的正方向向上,當xoy坐標系中x軸正方向向著y軸正方向轉動時為正值α時,也就是逆時針轉動,這時的轉換矩陣為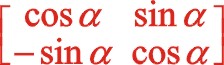 ,轉換矩陣左乘所研究的函數特征,形成了在x'oy'坐標系中新的函數關系式,這不改變該函數的本質屬性,但能夠幫助人們更清楚認識該函數的圖像,不同的視角得出的函數表達式是不相同的,但本質是相同的。因此圖(10)是正角45°的坐標系矩陣變換,其因子為
,轉換矩陣左乘所研究的函數特征,形成了在x'oy'坐標系中新的函數關系式,這不改變該函數的本質屬性,但能夠幫助人們更清楚認識該函數的圖像,不同的視角得出的函數表達式是不相同的,但本質是相同的。因此圖(10)是正角45°的坐標系矩陣變換,其因子為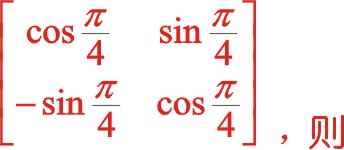
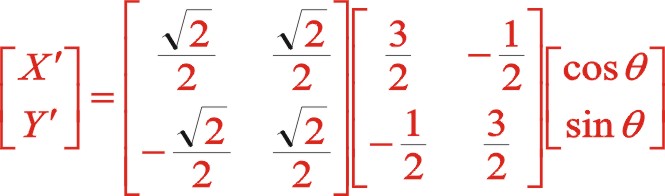
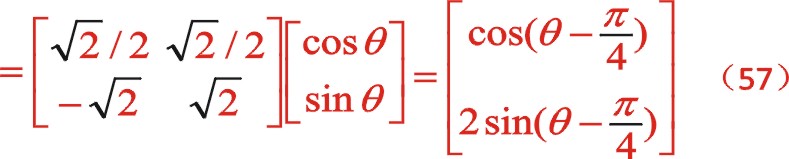
②二階慣性力的計算
這里先用傳統的三角函數來計算。
垂直方向:
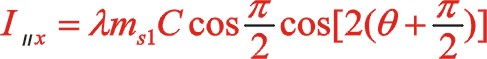
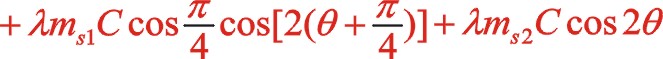
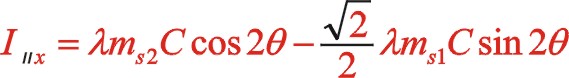

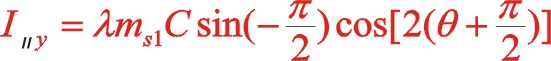
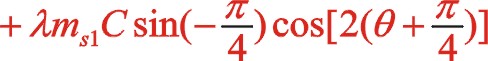

也可以采用復數分析法,下面簡單地寫出。二階慣性力用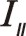 表示,下標Ⅱ代表二階。按照圖7從左到右的閱讀順序,其二階慣性力合力的構成如(11)式所表達
表示,下標Ⅱ代表二階。按照圖7從左到右的閱讀順序,其二階慣性力合力的構成如(11)式所表達
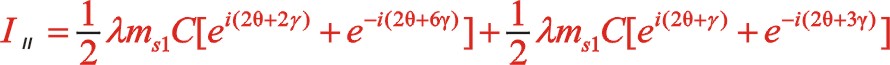

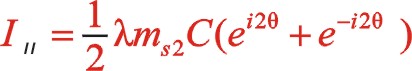
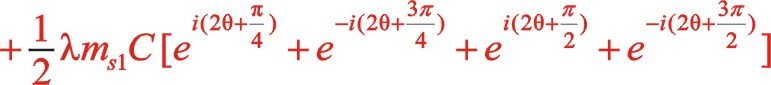
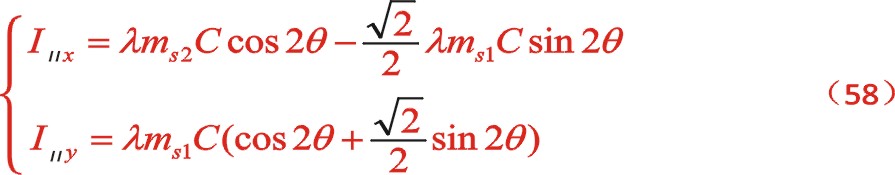
關于W型45°順轉二階慣性力也有下列的方程運算。
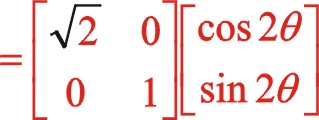

6.2用基礎理論分析圖11形式反時針轉動時慣性力
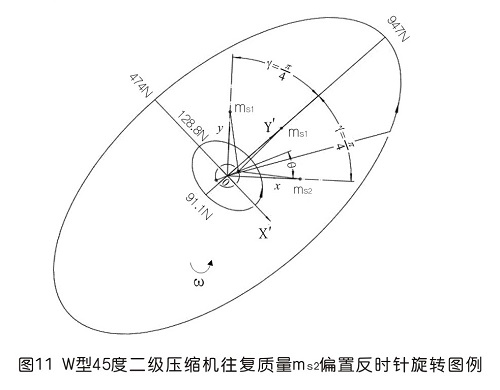
①一階慣性力的計算
同樣,一階慣性力合力的構成按圖11所示的構成,依次寫出如下
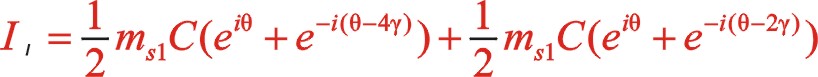

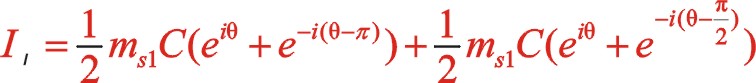

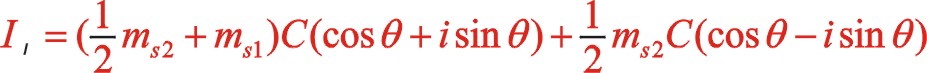
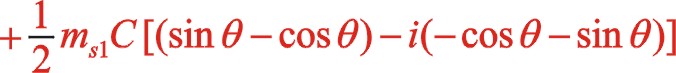
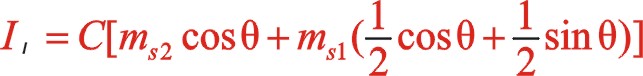

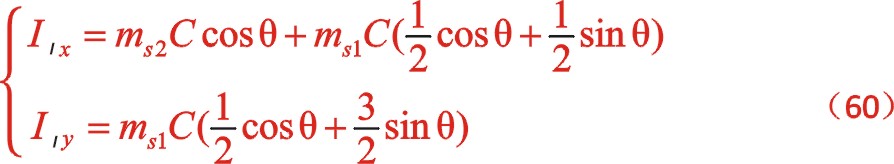
根據上一篇文章75°的文中分析,順、反旋轉時,角度“θ”用“— θ”代替,y方向也就是虛部的代數式“y”用“— y”代替這樣的二原則,則式(60)與式(55)比較起來,同樣適用這一原則。既適用于一階,也適用于二階。60°的情形也同樣適用,這里提及一下,有興趣的讀者可以回看一下。


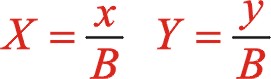

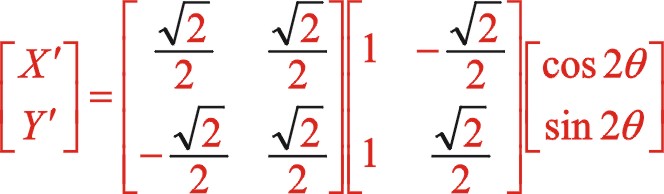
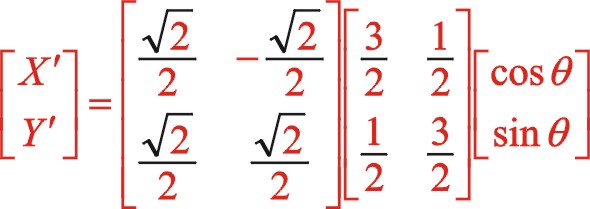
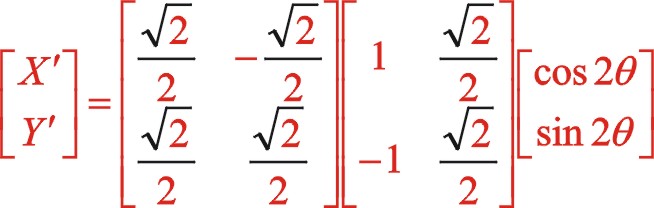
坐標系作負值45°變換,則
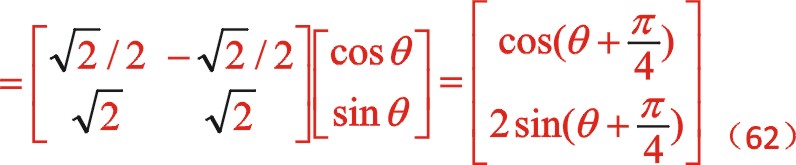
②二階慣性力的計算
二階慣性力合力的構成按圖11所示的構成,依次寫出如下
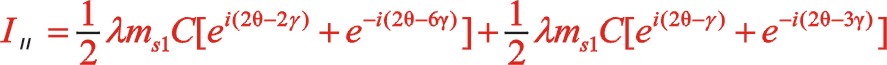

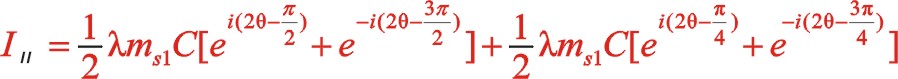
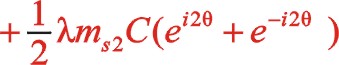
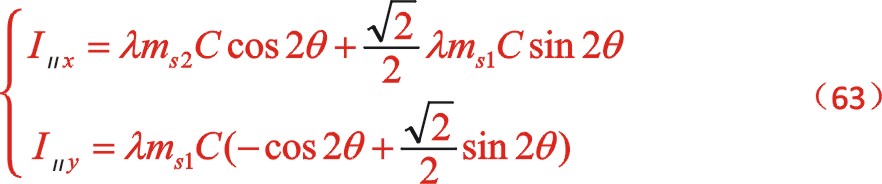
由上一篇文章75°的文中分析,順反旋轉時,角度“θ”用“— θ”代替,y方向也就是虛部的代數式“y”用“— y”代替這樣的二原則,則式(63)與式(58)比較起來,同樣適用這一原則。這可以檢驗運算過程的正確性,或者可能由于誤輸入加減符號導致的常識性錯誤。60°的二階慣性力表達式也遵循這個,有興趣的讀者可以回看一下。
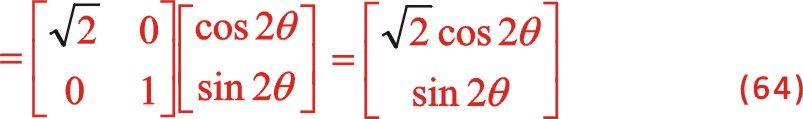
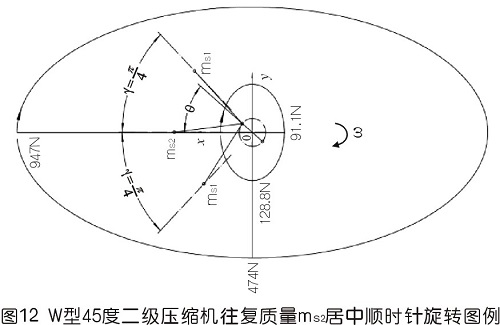
6.3用基礎理論分析圖12形式順時針轉動時慣性力
①一階慣性力的計算
一階慣性力合力的構成按圖12所示的構成,依次寫出如下
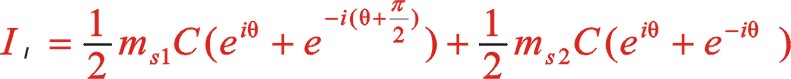
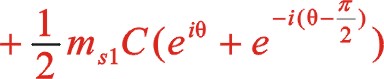


若兩質量相等,則可以得出W型45°壓縮機上述三種情形一階慣性力的橢圓的短長軸之比為0.5。
②二階慣性力的計算
二階慣性力合力的構成按圖12所示的構成,依次寫出如下
垂直方向:

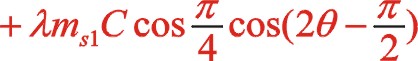
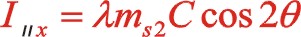

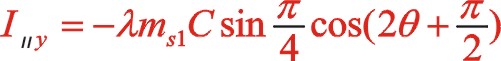
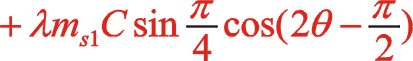


根據式(66),若兩質量相等,可得出W型45°壓縮機上述三種情形二階慣性力的橢圓的短長軸之比為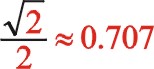 。
。
6.4圖12與圖10、圖11利用坐標系旋轉變換作出的公式的一致性推導
根據前述的理論,我們將圖12的坐標系順旋轉方向轉動45°后建立了新坐標系,也就是正角變換,這樣一來該坐標系就與圖10中一模一樣。我們所做的事是已知式(65)的方程,利用該式怎樣推導出式(56),以驗算理論推導過程的一致性。我們進行坐標系的旋轉變換,作如下
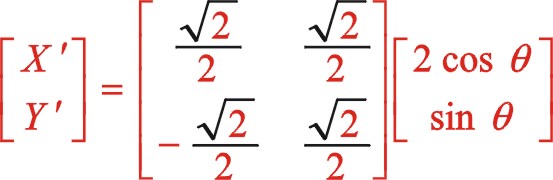
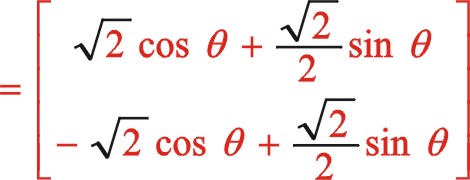
因為我們得到的式(56)是從偏置時開始計角度的,設重新建立新的坐標系后我們從偏置一邊的活塞時開始計及角度α,則上面的“θ”用“ 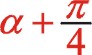 ”來代替,經運算后
”來代替,經運算后
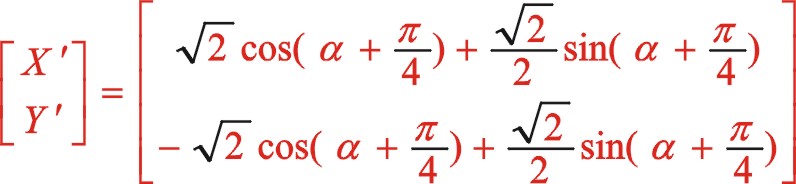
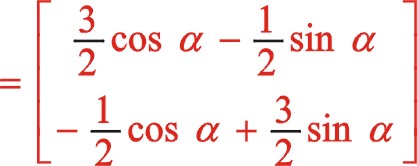
上式與式(56)一樣,所以得證。
由于圖12所畫的轉向是順時針,為弄明白坐標系的旋轉變換是正角變換還是負值變換,可以作圖11的鏡像圖,所以得到是負角變換,因鏡像后兩圖轉向已一致所以式(65)保持不變,考慮到新坐標系的開始角的度量關系所以“θ”用“ 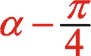 ”來代替,推導如下:
”來代替,推導如下:
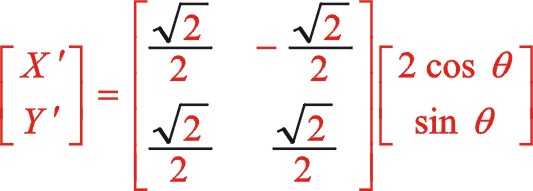
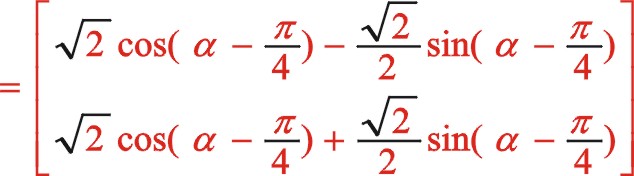
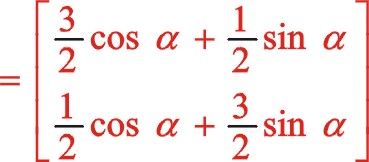
該式與式(61)保持一致,得證。
二階慣性力的代數式(66)、(58)、(63)也能進行一致性推導。其它角度也行,此處不展開讀者如若有興趣自行推導。下面簡單寫出該角度的二階慣性力推導方程式
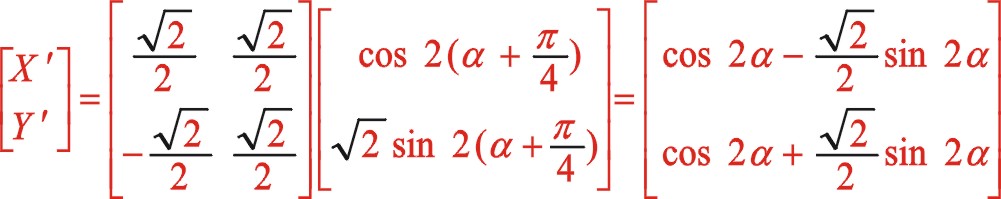
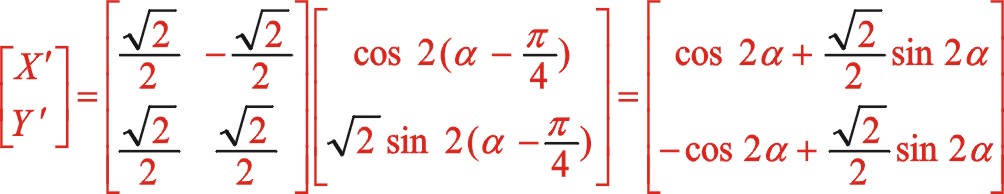
這種通過居中布置的參數方程推導出偏置時的參數方程,僅適用于ms2=ms1時,對于二者質量不相等的情形,不能夠通過坐標系的旋轉變換來推導,因為研究的方法可靈活而固有的結構ms2不能夠旋轉,更多的理論——橢圓的小偏轉理論、60°分布時橢圓大旋轉理論——似乎也能支持該種算法。因此,還是用傳統的方法計算各自的方程來得更直接些。
進行這些運算,可以加強理論的縝密性,可以檢驗推導過程的正確性,這些都是基于對數學中線性代數學科的研究、基于平時的善于發現,基于前述的基礎理論中的正方向理論。
6.5總結
本處以安徽華晶機械有限公司生產的WW-0.9/10B-Q型全無油二級空壓機為模版,假定氣缸夾角為45°,計算其一、二階往復慣性力。此處先假定三列往復質量相等,即ms為1.8kg,曲柄半徑為0.0375m,曲柄半徑連桿比λ為37.5/195,角速度ω為2π×(800/60)rad/s,現將上述結構參數分別代入上文中所列的相關公式中,運用計算機內EXCEL程序列表、繪圖計算分析,計算的結果繪制在上圖的圖10、圖11、圖12中,可以得到以下結論:
1)一階慣性力由60°分布的圓變成橢圓,且橢圓的短長軸之比由1變成0.5,如果方向一致則是由1變成2;平均值由711N變成731N,有所增大;方向由跟隨變成近似跟隨。圖10、11中已畫出一、二階慣性力剛開始時的矢量線,用橢圓斷開表示,圖12中反映一階慣性力在某個時候有重合的可能。
2)二階慣性力說明,其橢圓短長軸之比由0.333變成0.707。力的平均值由96.9N變成110.8N,有所增加。方向初看是亂的,但很有規律,因為三角函數是周期函數。這個規律待人們去認識、研究、發現、找尋合適的機構來平衡。
3)當ms2≠ms1時,60°分布一階慣性力在ms2列方向形成橢圓的對稱軸,而45°不是,說明角度優先于質量,說明W型時,60°分布是最優的。從式(9)的復數表達式、式(10)的幾何表達式中可以看出,60°分布時一階慣性力長短軸與角度無關,僅與質量有關,這與上也是吻合的。
4)它們的共同點是,曲柄轉1周,一階慣性力也轉1周,且同向;二階慣性力轉2周,也同向。
若ms2≠ms1,會引起圖10、圖11、圖12中兩個橢圓有所歧化,或偏轉,兼帶擴壓,使其相位、幅值有微量變化。
〈注:本文未完待續,更多精彩見下期!〉
參考文獻
(1)宋瑞林,氣缸夾角為60°的V6車用發動機往復慣性力的平衡分析,[J],汽車技術,1988.8
(2)李松虎,3W型活塞壓縮機往復慣性力的分析,[J],壓縮機技術,1987.3
(3)陸鵬程,張光勝,三星型壓縮機振動問題研究,[J],安徽工程科技學院學報,2009.1
(4)王再順,夾角為90°的V型壓縮機往復慣性力平衡的探討,[J],壓縮機技術,1986.2
作者簡介
陸鵬程,男,安徽桐城人,海軍工程大學在職碩士畢業。現在中國人民解放軍第四八一二工廠,安徽華晶機械有限公司工作,高級工程師。研究方向:壓縮機研究與強度設計。
來源:本站原創
【壓縮機網】〈接上期——〉
六、夾角γ為45°的計算
6.1用基礎理論分析圖10形式順時針轉動時慣性力

![]()
①一階慣性力的計算
一階慣性力用![]() 表示,下標
表示,下標![]() 代表一階。按照圖10從左到右的閱讀順序,其一階慣性力合力的構成如(7)式所表達
代表一階。按照圖10從左到右的閱讀順序,其一階慣性力合力的構成如(7)式所表達
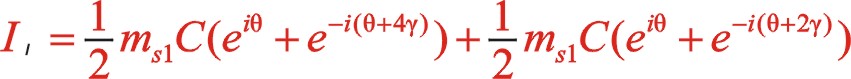

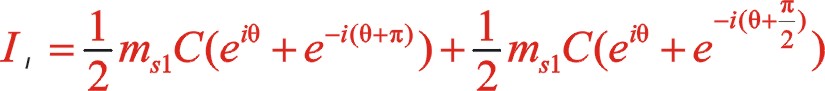
 、
、

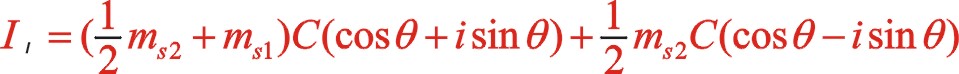


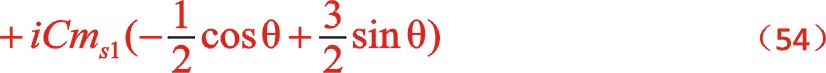

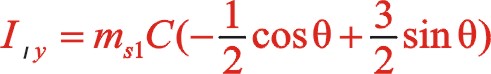
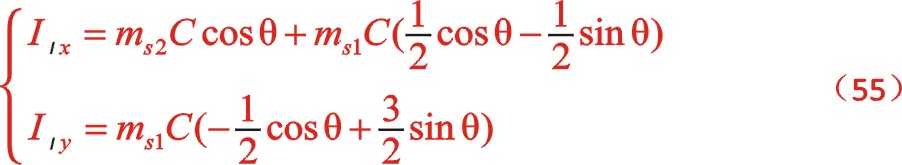


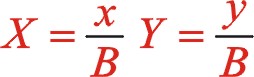

坐標系如圖所示順轉45°后,變成了氣缸對稱分布的主方向。一般的,根據坐標系的旋轉變換(不是坐標的旋轉變換,根據網絡百度上發布的信息仔細甄別:坐標的旋轉變換是指只有一個坐標系,有一個向量逆時針旋轉α后變成一個新的向量,新的點的坐標也可以采用矩陣運算來完成,而其矩陣運算的因子卻為![]() ,經矩陣的乘法運算后形成新的值還在原來的坐標系中度量,這一點與計算機圖學中作“X=X+1”賦值運算一樣。可以說坐標的旋轉變換與坐標系的旋轉變換是一對互為逆運算),有這樣的理論:對于標準的直角坐標系即x軸正方向向右,y軸的正方向向上,當xoy坐標系中x軸正方向向著y軸正方向轉動時為正值α時,也就是逆時針轉動,這時的轉換矩陣為
,經矩陣的乘法運算后形成新的值還在原來的坐標系中度量,這一點與計算機圖學中作“X=X+1”賦值運算一樣。可以說坐標的旋轉變換與坐標系的旋轉變換是一對互為逆運算),有這樣的理論:對于標準的直角坐標系即x軸正方向向右,y軸的正方向向上,當xoy坐標系中x軸正方向向著y軸正方向轉動時為正值α時,也就是逆時針轉動,這時的轉換矩陣為![]() ,轉換矩陣左乘所研究的函數特征,形成了在x'oy'坐標系中新的函數關系式,這不改變該函數的本質屬性,但能夠幫助人們更清楚認識該函數的圖像,不同的視角得出的函數表達式是不相同的,但本質是相同的。因此圖(10)是正角45°的坐標系矩陣變換,其因子為
,轉換矩陣左乘所研究的函數特征,形成了在x'oy'坐標系中新的函數關系式,這不改變該函數的本質屬性,但能夠幫助人們更清楚認識該函數的圖像,不同的視角得出的函數表達式是不相同的,但本質是相同的。因此圖(10)是正角45°的坐標系矩陣變換,其因子為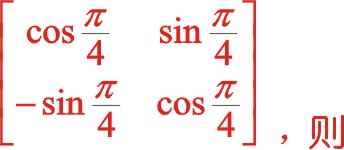

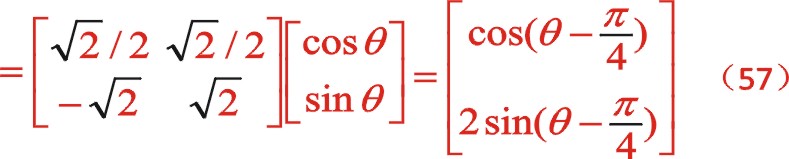
②二階慣性力的計算
這里先用傳統的三角函數來計算。
垂直方向:
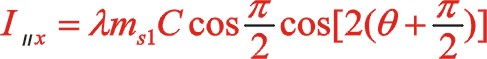
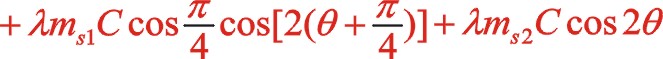
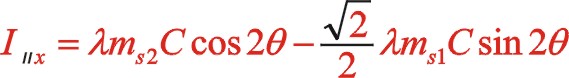

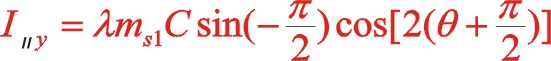
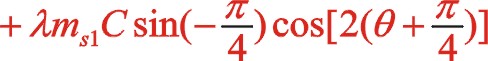

也可以采用復數分析法,下面簡單地寫出。二階慣性力用![]() 表示,下標Ⅱ代表二階。按照圖7從左到右的閱讀順序,其二階慣性力合力的構成如(11)式所表達
表示,下標Ⅱ代表二階。按照圖7從左到右的閱讀順序,其二階慣性力合力的構成如(11)式所表達
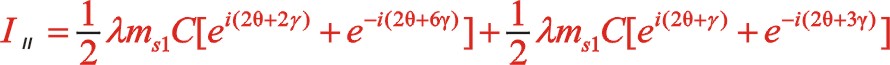

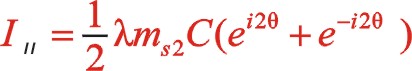
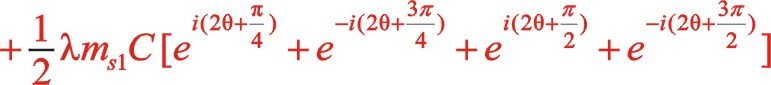
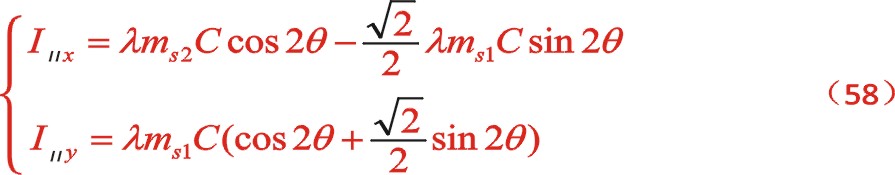
關于W型45°順轉二階慣性力也有下列的方程運算。

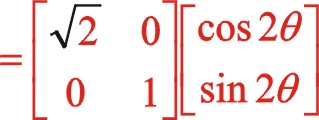

6.2用基礎理論分析圖11形式反時針轉動時慣性力

①一階慣性力的計算
同樣,一階慣性力合力的構成按圖11所示的構成,依次寫出如下
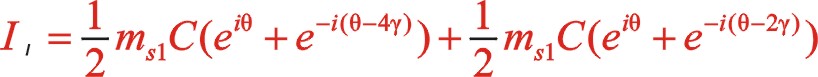

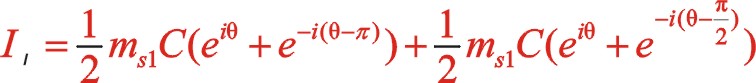

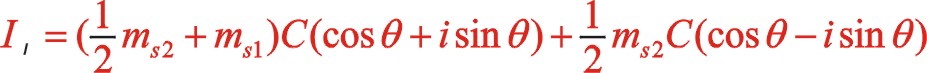
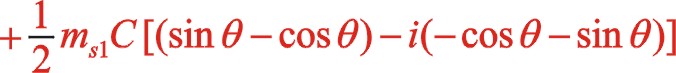
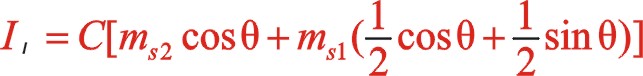

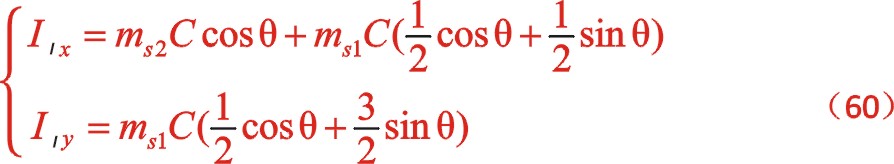
根據上一篇文章75°的文中分析,順、反旋轉時,角度“θ”用“— θ”代替,y方向也就是虛部的代數式“y”用“— y”代替這樣的二原則,則式(60)與式(55)比較起來,同樣適用這一原則。既適用于一階,也適用于二階。60°的情形也同樣適用,這里提及一下,有興趣的讀者可以回看一下。


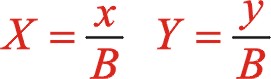

坐標系作負值45°變換,則

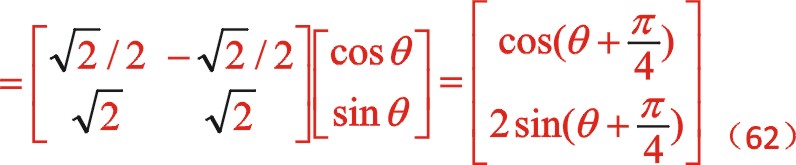
②二階慣性力的計算
二階慣性力合力的構成按圖11所示的構成,依次寫出如下
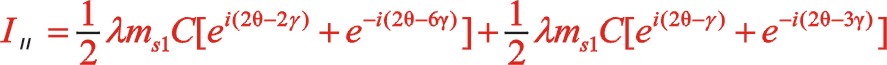

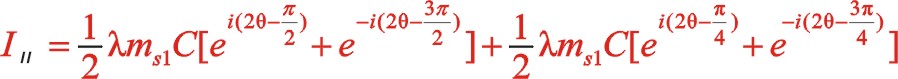
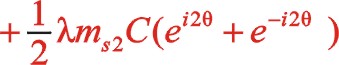
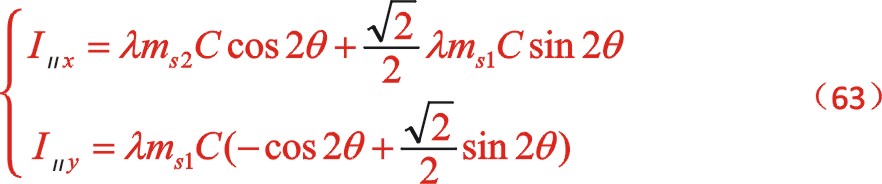
由上一篇文章75°的文中分析,順反旋轉時,角度“θ”用“— θ”代替,y方向也就是虛部的代數式“y”用“— y”代替這樣的二原則,則式(63)與式(58)比較起來,同樣適用這一原則。這可以檢驗運算過程的正確性,或者可能由于誤輸入加減符號導致的常識性錯誤。60°的二階慣性力表達式也遵循這個,有興趣的讀者可以回看一下。

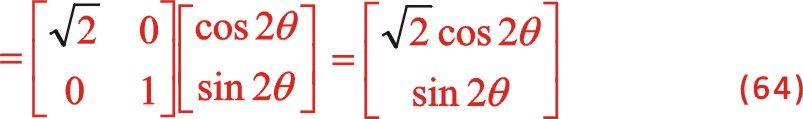
6.3用基礎理論分析圖12形式順時針轉動時慣性力

①一階慣性力的計算
一階慣性力合力的構成按圖12所示的構成,依次寫出如下
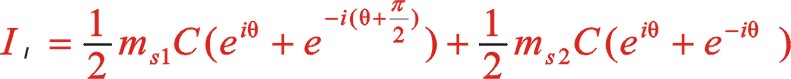
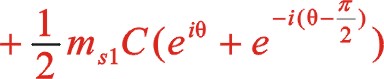


若兩質量相等,則可以得出W型45°壓縮機上述三種情形一階慣性力的橢圓的短長軸之比為0.5。
②二階慣性力的計算
二階慣性力合力的構成按圖12所示的構成,依次寫出如下
垂直方向:

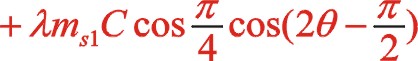
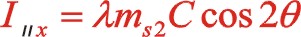

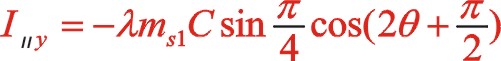
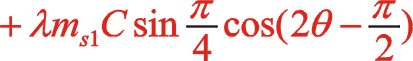


根據式(66),若兩質量相等,可得出W型45°壓縮機上述三種情形二階慣性力的橢圓的短長軸之比為![]() 。
。
6.4圖12與圖10、圖11利用坐標系旋轉變換作出的公式的一致性推導
根據前述的理論,我們將圖12的坐標系順旋轉方向轉動45°后建立了新坐標系,也就是正角變換,這樣一來該坐標系就與圖10中一模一樣。我們所做的事是已知式(65)的方程,利用該式怎樣推導出式(56),以驗算理論推導過程的一致性。我們進行坐標系的旋轉變換,作如下

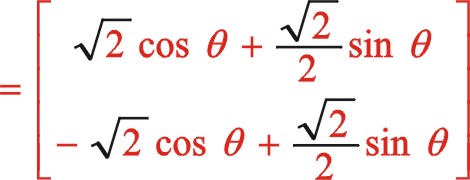
因為我們得到的式(56)是從偏置時開始計角度的,設重新建立新的坐標系后我們從偏置一邊的活塞時開始計及角度α,則上面的“θ”用“ ![]() ”來代替,經運算后
”來代替,經運算后
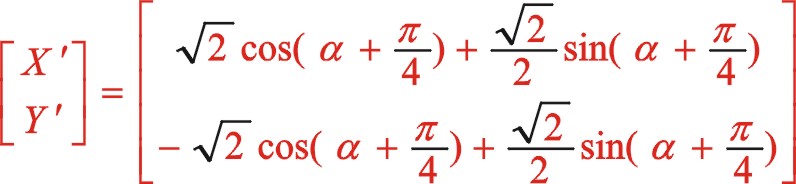
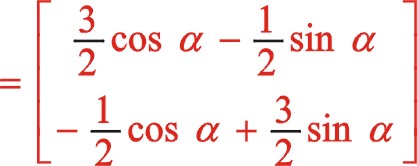
上式與式(56)一樣,所以得證。
由于圖12所畫的轉向是順時針,為弄明白坐標系的旋轉變換是正角變換還是負值變換,可以作圖11的鏡像圖,所以得到是負角變換,因鏡像后兩圖轉向已一致所以式(65)保持不變,考慮到新坐標系的開始角的度量關系所以“θ”用“ ![]() ”來代替,推導如下:
”來代替,推導如下:
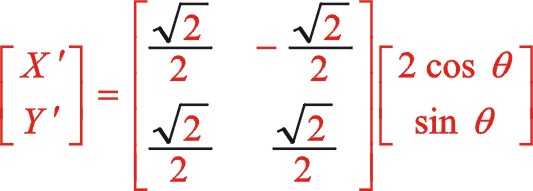
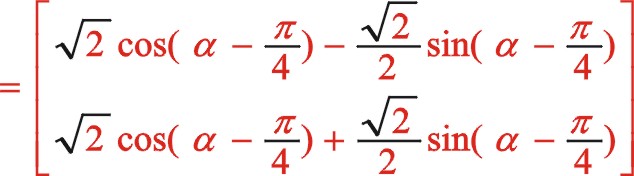
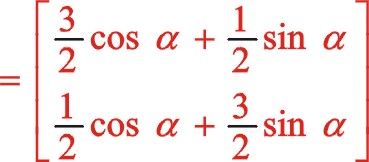
該式與式(61)保持一致,得證。
二階慣性力的代數式(66)、(58)、(63)也能進行一致性推導。其它角度也行,此處不展開讀者如若有興趣自行推導。下面簡單寫出該角度的二階慣性力推導方程式
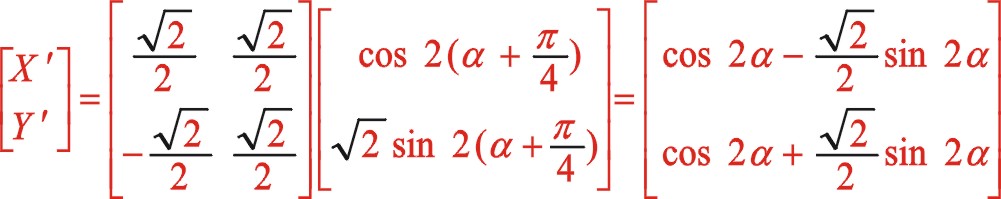
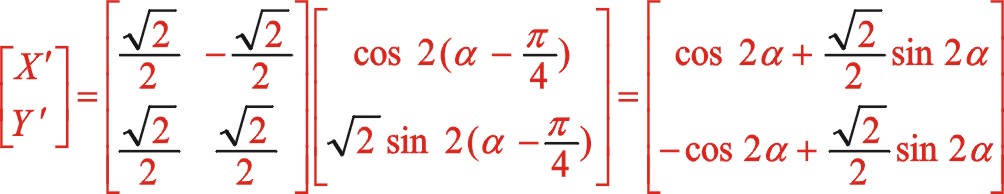
這種通過居中布置的參數方程推導出偏置時的參數方程,僅適用于ms2=ms1時,對于二者質量不相等的情形,不能夠通過坐標系的旋轉變換來推導,因為研究的方法可靈活而固有的結構ms2不能夠旋轉,更多的理論——橢圓的小偏轉理論、60°分布時橢圓大旋轉理論——似乎也能支持該種算法。因此,還是用傳統的方法計算各自的方程來得更直接些。
進行這些運算,可以加強理論的縝密性,可以檢驗推導過程的正確性,這些都是基于對數學中線性代數學科的研究、基于平時的善于發現,基于前述的基礎理論中的正方向理論。
6.5總結
本處以安徽華晶機械有限公司生產的WW-0.9/10B-Q型全無油二級空壓機為模版,假定氣缸夾角為45°,計算其一、二階往復慣性力。此處先假定三列往復質量相等,即ms為1.8kg,曲柄半徑為0.0375m,曲柄半徑連桿比λ為37.5/195,角速度ω為2π×(800/60)rad/s,現將上述結構參數分別代入上文中所列的相關公式中,運用計算機內EXCEL程序列表、繪圖計算分析,計算的結果繪制在上圖的圖10、圖11、圖12中,可以得到以下結論:
1)一階慣性力由60°分布的圓變成橢圓,且橢圓的短長軸之比由1變成0.5,如果方向一致則是由1變成2;平均值由711N變成731N,有所增大;方向由跟隨變成近似跟隨。圖10、11中已畫出一、二階慣性力剛開始時的矢量線,用橢圓斷開表示,圖12中反映一階慣性力在某個時候有重合的可能。
2)二階慣性力說明,其橢圓短長軸之比由0.333變成0.707。力的平均值由96.9N變成110.8N,有所增加。方向初看是亂的,但很有規律,因為三角函數是周期函數。這個規律待人們去認識、研究、發現、找尋合適的機構來平衡。
3)當ms2≠ms1時,60°分布一階慣性力在ms2列方向形成橢圓的對稱軸,而45°不是,說明角度優先于質量,說明W型時,60°分布是最優的。從式(9)的復數表達式、式(10)的幾何表達式中可以看出,60°分布時一階慣性力長短軸與角度無關,僅與質量有關,這與上也是吻合的。
4)它們的共同點是,曲柄轉1周,一階慣性力也轉1周,且同向;二階慣性力轉2周,也同向。
若ms2≠ms1,會引起圖10、圖11、圖12中兩個橢圓有所歧化,或偏轉,兼帶擴壓,使其相位、幅值有微量變化。
〈注:本文未完待續,更多精彩見下期!〉
參考文獻
(1)宋瑞林,氣缸夾角為60°的V6車用發動機往復慣性力的平衡分析,[J],汽車技術,1988.8
(2)李松虎,3W型活塞壓縮機往復慣性力的分析,[J],壓縮機技術,1987.3
(3)陸鵬程,張光勝,三星型壓縮機振動問題研究,[J],安徽工程科技學院學報,2009.1
(4)王再順,夾角為90°的V型壓縮機往復慣性力平衡的探討,[J],壓縮機技術,1986.2
作者簡介
陸鵬程,男,安徽桐城人,海軍工程大學在職碩士畢業。現在中國人民解放軍第四八一二工廠,安徽華晶機械有限公司工作,高級工程師。研究方向:壓縮機研究與強度設計。
來源:本站原創











網友評論
條評論
最新評論