一、序言
【壓縮機網】W型壓縮機在我們的日常生活中非常常見。我廠目前已有的該類產品有0.5/14,0.9/10,1.25/10,1.8/8,CW480/40系列等。我們在這些年的生產和試制過程中發現:每種機器在初始試制中,由于三列的活塞等往復質量控制不理想,機器的設計轉速都在1000r/min左右,或許是剛開始設計活塞重量時欠考慮,機器試制時振動烈度都較高。隨著后期該種機器的批量投產,鋁活塞的質量也在強度允許范圍內有所下降,工程技術人員也意識到多級壓縮時不同級的活塞往復質量的偏差區間要從嚴考慮,現在W型機器的振動烈度比試制初期改善了許多。
本文以單曲拐、W型角度式壓縮機為例,由于往復質量的差異,從理論上分析推導出機器的一、二階往復慣性力的公式,該慣性力作用在曲軸箱體中心點上,該變化的慣性力的矢端在曲軸的運動平面上形成了慣性力的矢端軌跡力圖。根據該公式,提出合適的平衡一、二階往復慣性力的措施,用以推動國內的壓縮機的升級換代。
二、基礎理論
1.正方向的問題
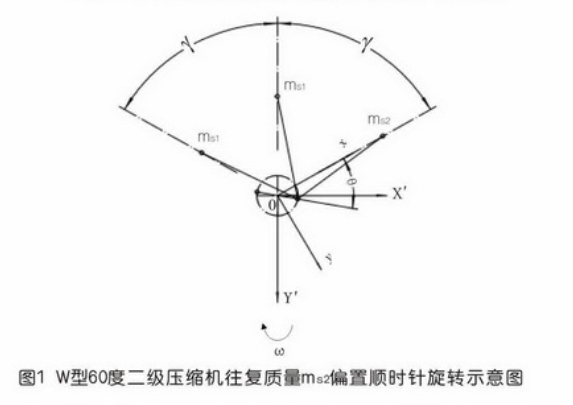
W型壓縮機的三列連桿并列于同一的曲拐軸上,如圖1所示,為通用性計,該圖列之間夾角沒有畫成60°。我們這里考慮兩級壓縮機,它有兩個一級一個二級,設一級的往復部件質量為ms1,二級往復部件質量為ms2,以圖示的右邊的一列ms2為基準建立直角坐標系moy,規定投影到曲柄方向為x軸,與曲柄垂直的方向為y軸。這里規定x軸正方向是由機器中心向外指,這與壓縮機中將連桿受拉伸規定為正值相吻合,壓縮機動力計算時也將曲柄在上死點位置時運動部件受到的往復慣性力為正的最大值。y軸的正方向規定為將x軸順旋轉方向轉一直角方向為其正方向。這樣的規定都是為了方便計算,為后面的各種計算打下基礎,也更容易發現規律。
2.研究手段問題
本文采用歐拉公式研究三列慣性力矢量的合力問題,將教科書上推導過程中采用垂直和水平方向兩個式子合并成一個式子,這里規定x軸代表向量的實部,y軸代表向量的虛部,二者連接采用虛數單位i來連接。運用到的相關公式如下:
 (1)
(1)
 為工程指數,
為工程指數, 為虛數單位,
為虛數單位, 為曲柄轉角,單位為弧度,規定順時針旋轉方向為正值,θ為變量函數。該式子描述的也就是單位圓。
為曲柄轉角,單位為弧度,規定順時針旋轉方向為正值,θ為變量函數。該式子描述的也就是單位圓。
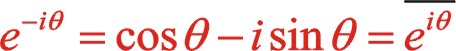 (2)
(2)
該式子也是上復數的共軛復數。

一階慣性力是余弦函數,本文將一對互為共軛的復數的平均值來研究一、二階慣性力。
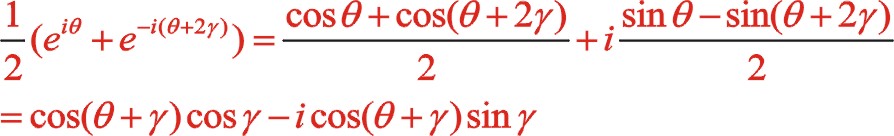 (4)
(4)
它巧妙地運用到兩個不同相位的歐拉函數的代數和來研究慣性力的投影問題。式子的右邊正好是圖示中中間列一階慣性力投影到xoy坐標系上兩個方向上兩個力的大小,根據前面規定了x,y軸的正方向,注意到上式的虛部應為負值。該式的“ ”用“—
”用“— ”代替后形成新的公式后文中也會運用到它。
”代替后形成新的公式后文中也會運用到它。
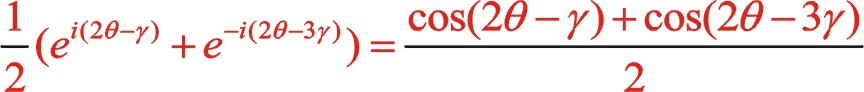
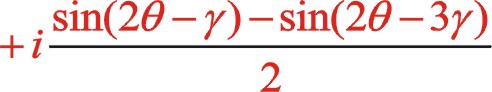
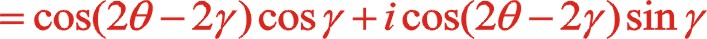 (5)
(5)
該式子是圖2中間列二階慣性力投影到xoy坐標系上兩個方向上兩個力的大小。該式的“  ”用“—
”用“—  ”代替后形成新的公式就是圖1中二階慣性力的計算公式。
”代替后形成新的公式就是圖1中二階慣性力的計算公式。
3.研究切入點問題
本文研究慣性力的計算公式及其圖像,顧及三列不同的往復質量對計算公式的影響,所以研究的起始點非常重要。文章分析了兩種往復質量的計算公式,為計算方便,通常θ角的計入零點規定為ms2列活塞處于上死點的位置。文中得到的計算公式與選擇上面的計入零點無關。
三、計算過程
文中分析了ms2列活塞偏置一邊時順時針及反時針旋轉的一、二階往復慣性力的計算公式,對ms2列活塞置于中間時旋轉方向已不重要了,文中也分析了若順時針旋轉時計算公式。三列活塞套入曲柄銷的先后順序形成的慣性力矩也各不相同,由于微小,本文不作研究。文中假設三列都在同一個往復運動平面上往復慣性力合成后的矢端軌跡圖像。
1.用基礎理論分析圖1形式順時針轉動時慣性力
 (6)
(6)
r為曲柄半徑。ω為旋轉角速度,以弧度計入計算。C為后文列出的公式書寫方便引入的記號。
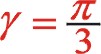
1.1一階慣性力的計算
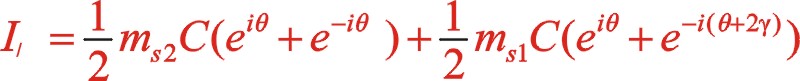
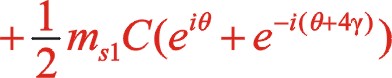 (7)
(7)
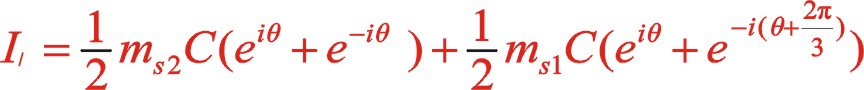
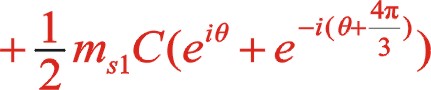

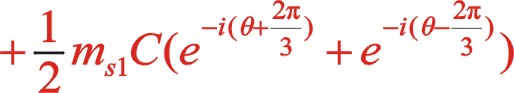
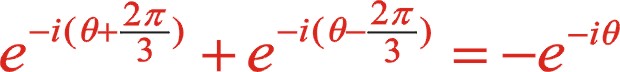
(8)
該式用到了三角函數的和差化積公式。
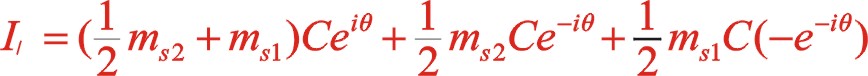
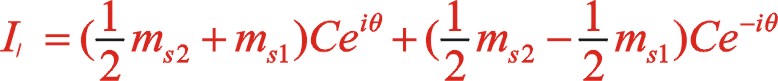
 (9)
(9)
上式就是W型夾角60°一階往復慣性力復數表達式。
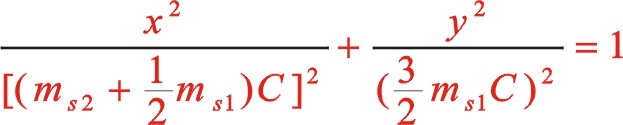 (10)
(10)
上式表明,一階慣性力矢端軌跡是一橢圓,變化的周期和曲軸旋轉的周期相同。該橢圓的圖像在運動平面上相當于將標準橢圓順時針旋轉了30°,若ms2>ms1,長半軸為(ms2+0.5ms1)C,短半軸為(1.5ms1)C;若ms2=ms1,橢圓退化成圓,半徑為(1.5ms1)C。
1.2二階慣性力的計算
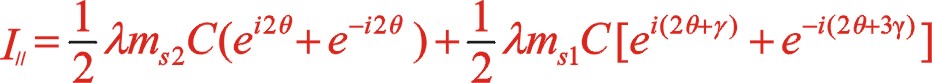
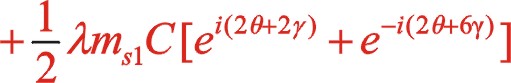 (11)
(11)
式中λ為曲柄半徑連桿比。
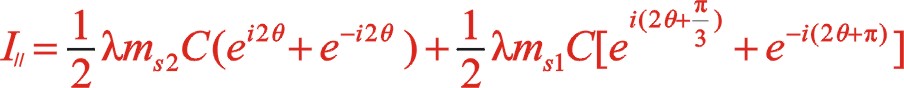
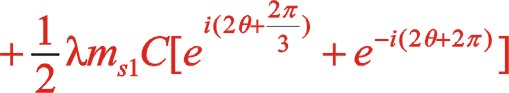

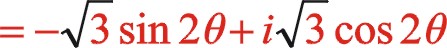 (12)
(12)
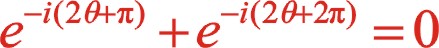 (13)
(13)
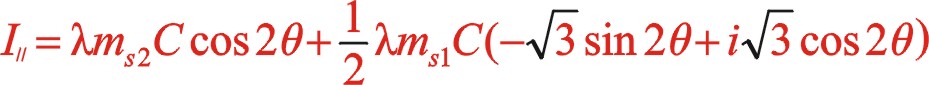
 (14)
(14)
這是W型夾角60°二階往復慣性力復數表達式。
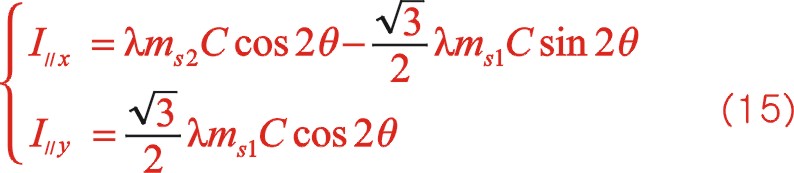
這也是二階慣性力參數方程的表達式。
為尋找上方程所描述的圖像,先假定兩個往復質量相等,利用尋找兩個變量的二次多項式方程方法和矩陣轉換法來進行。
 (16)
(16)
 (17)
(17)
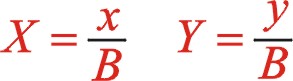
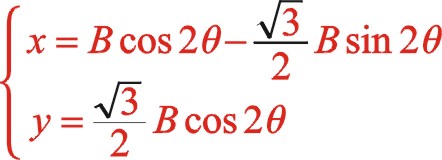
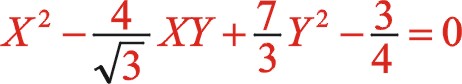 (18)
(18)
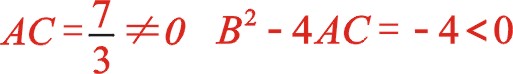
根據線性代數中二次多項式的判別式定理,滿足上兩個條件,所以二階慣性力也是一個橢圓。
坐標系順轉30°后,由于y軸在標準直角坐標的對面,相當于坐標系逆時針旋轉30°,作坐標系的矩陣變換的因子為
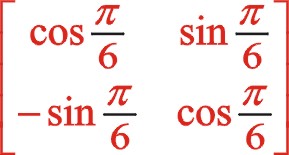
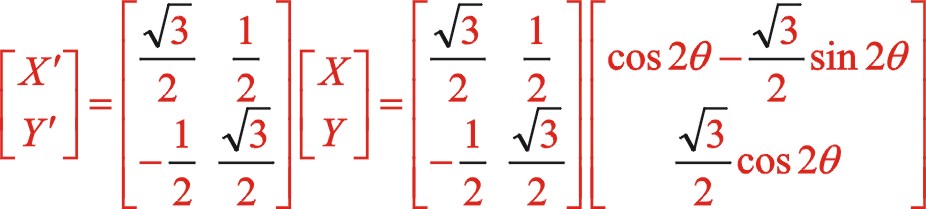
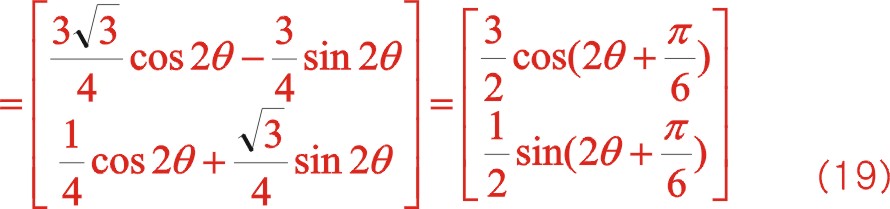
上式清晰地表明二階慣性力的軌跡是橢圓,變化的周期是曲軸旋轉的周期的一半。經坐標系的旋轉變換后的參數方程表明:該橢圓的長半軸是短半軸的3倍,不論是在xoy坐標系還是在x'oy'坐標系中,其橢圓的長半軸始終在水平方向,這與三列活塞在旋轉平面的分布緊密聯系,后文還分析表明,不論ms2處于偏置還是中間位置,不論旋轉方向,二階慣性力矢端力圖始終是橢圓,該橢圓的長軸始終處于水平方向,不過其相位變化比較復雜,式(19)可以看出θ為30°時,力矢到達該橢圓的短半軸位置,這兩個矢量不在同一方向成90°,θ為 — 15°時,力矢到達該橢圓的長半軸位置,這兩個矢量不在同一方向成45°。二階慣性力的變化比曲軸自身旋轉變化快一倍。
2.用基礎理論分析圖2形式反時針轉動時慣性力
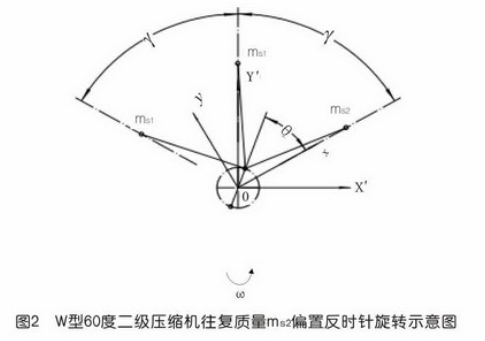
2.2一階慣性力的計算
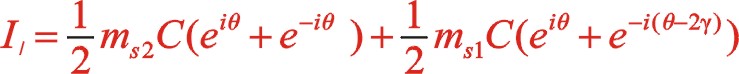
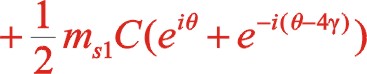 (20)
(20)
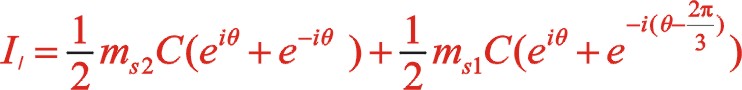
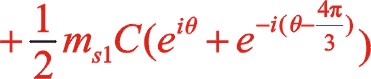
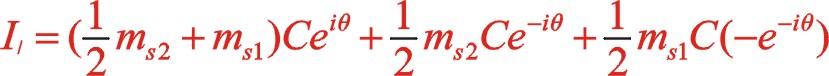
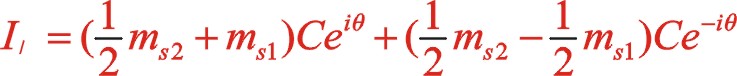

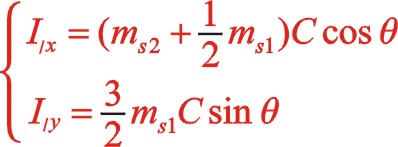
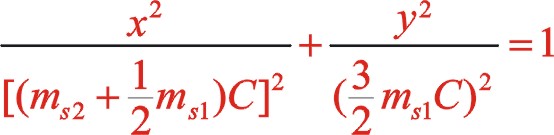
(21)
該式表明反時針旋轉時,一階慣性力復數方程和直角坐標方程形式上與順時針旋轉時完全相同,說明W型60°布置時,軌跡力圖與轉向無關,軌跡力矢的方向始終在曲柄轉動方向矢附近。當二者質量相等時,就成圓的變化,能夠在曲柄的反方向加一合適的平衡重,達到完全平衡掉一階往復慣性力。
2.2二階慣性力的計算
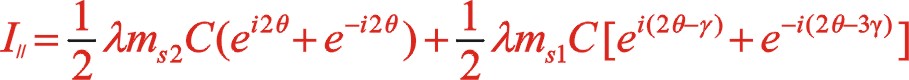
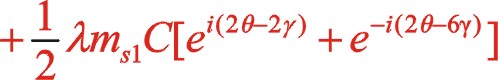 (22)
(22)
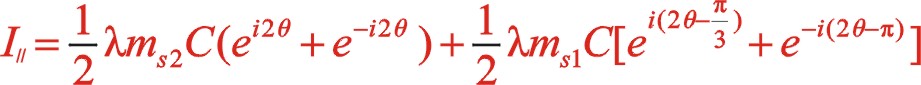
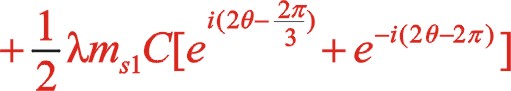
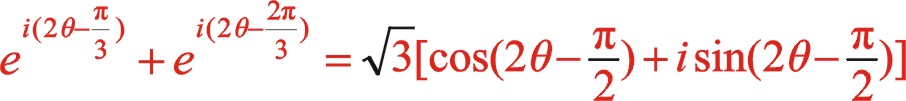
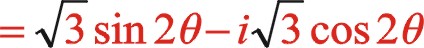




(23)
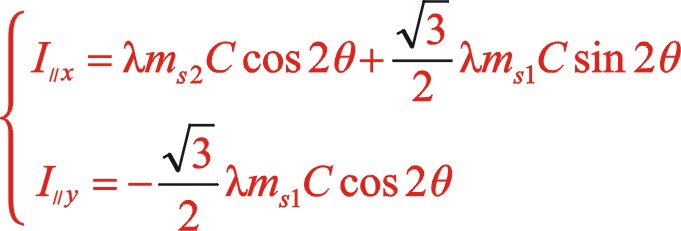
(24)
上式表明反時針旋轉時,二階慣性力直角坐標方程形式上與順時針旋轉時不同,說明換一個方向旋轉時,需要另一種方程描述二階慣性力的表現形式。后文的計算表明,它們的軌跡力圖是相同的。文章從理論提供了該力矢的數學表達式,希望能找到一種合適的機構加裝上也能夠平衡掉二階往復慣性力。
下面仿上面的假設,推導出它是一橢圓的依據。


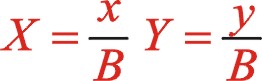
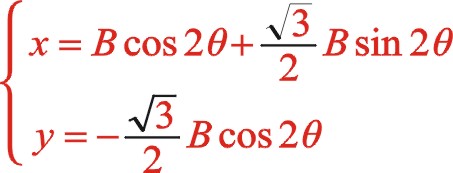
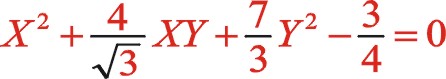
(25)
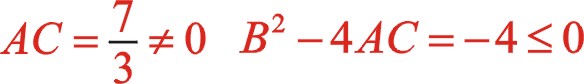
坐標系順轉30°后
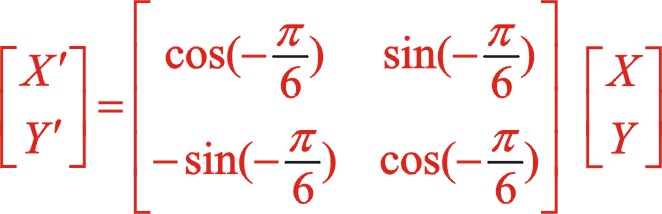
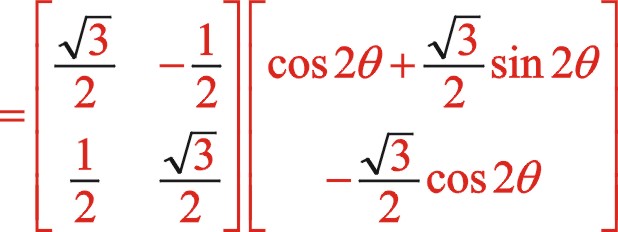
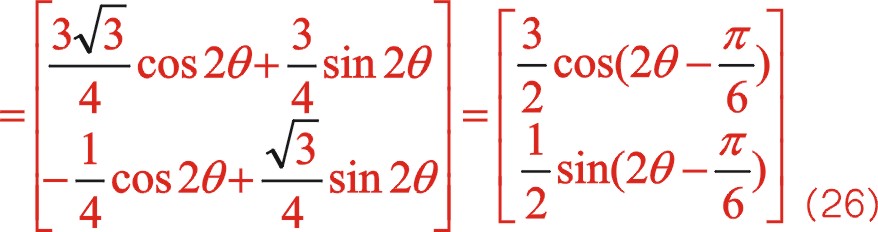
3.用基礎理論分析圖3形式順時針轉動時慣性力
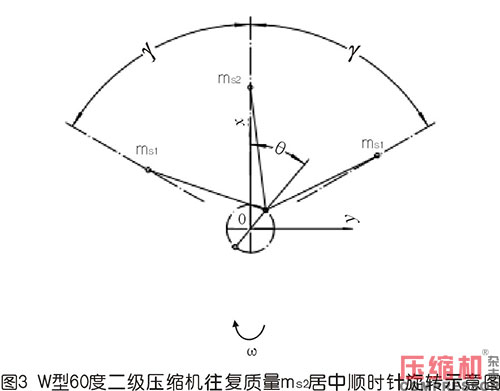
3.1一階慣性力的計算
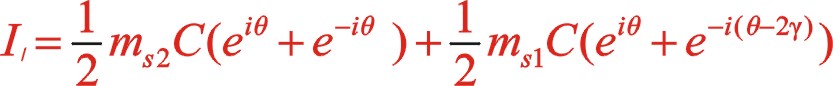
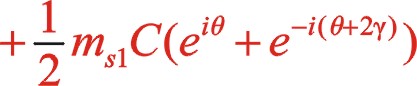
(27)
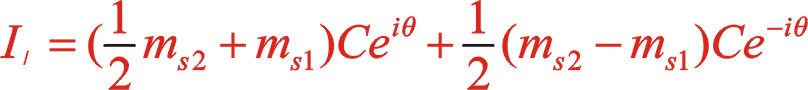

(28)
一階力矢成橢圓變化。
3.2二階慣性力的計算
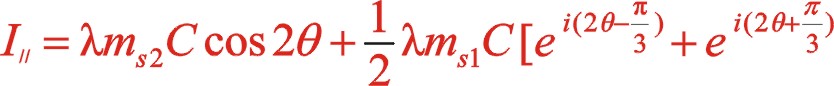
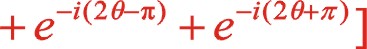
(29)
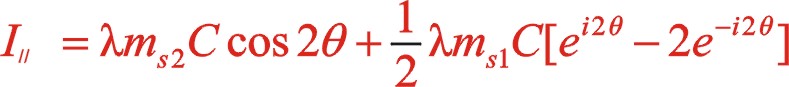

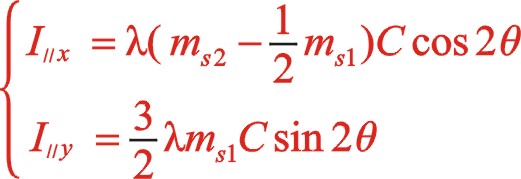
(30)
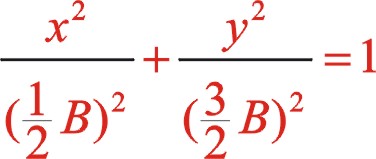
(31)
二階力矢也成橢圓變化,這種布置θ為0°時,力矢到達該橢圓的短半軸位置,曲柄方向矢與二階力矢在同一方向。
3.3討論
對于這種如圖3所示分布的機器,由式(28)、(30)可知:
①當ms2=ms1時,一階慣性力成圓的分布,二階慣性力成長短軸之比為3:1橢圓的分布;
②當ms2=2ms1時,一階慣性力成長短軸之比為5:3橢圓的分布,二階慣性力成圓的分布。
4.總結
從上面的三種情況分析和計算,可以得出W型60°布置有兩個ms1和一個ms2往復質量時有以下結論:
4.1一階慣性力是一橢圓,ms2列中心線是該橢圓的一個對稱軸方向,不論ms1、ms1、ms2在運動平面上如何分布,若ms2>ms1,則長軸在ms2列方向,反之則短軸在ms2列方向。
4.2二階慣性力也是一橢圓,若ms1=ms2,不論采用上面三種情況的特殊情形來計算,該橢圓的長軸始終在水平方向,短軸在豎直方向,并且長半軸是短半軸的3倍。若ms1≠ms2,則會將原來標準的橢圓作一適量旋轉,長短半軸的數值也會作微量變化。
四、舉例分析
本文以安徽華晶機械有限公司生產的WW-0.9/10B-Q型全無油空壓機為例分析W型60°二級壓縮機的一、二階往復慣性力。其中一級往復質量ms1為1.82kg,二級往復質量ms2為1.76kg,曲柄半徑為0.0375m,曲柄半徑連桿比λ為37.5/195,角速度ω為2π×(800/60)rad/s。現將上述結構參數分別代入上文中所列的相關公式中,運用計算機內EXCEL程序列表、繪圖計算分析,其結果如下:
1)按圖1形式作順時針轉動,其一、二階慣性力矢端力圖如圖4所示。
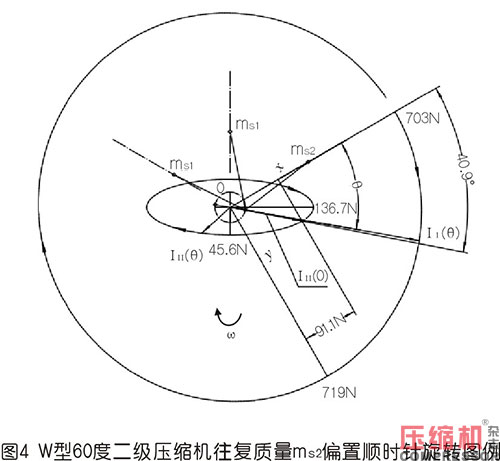
計算結果表明:當按照圖4所示建立的直角坐標系xoy后,按照順時針轉θ角后,一階往復慣性力如IⅠ(θ)所示,它是一個橢圓,二階往復慣性力如IⅡ(θ)所示,它也是一個很明顯的橢圓。一階慣性力的短半軸、長半軸為703N、719N,短軸在x軸方向上,該橢圓旋轉30°后形成標準橢圓。二階慣性力圖是按照總往復質量不變,三列往復質量相等繪制的(下同),即ms1=ms2=1.8kg,它是一個標準的橢圓,二階慣性力的長半軸、短半軸為136.7N、45.6N,長軸始終在水平方向,長短軸之比為3:1。圖中還顯示了當θ=0°,二階慣性力的向量是IⅡ(0),在x軸上刻度是91.1N,也就是式(11)中θ為0時的實部,該向量與x軸交角為40.9°,也就是說,初始的二階慣性力向量與曲柄矢不重合。當曲軸旋轉一周時,二階慣性力是從IⅡ(0)位置開始沿著其二階力橢圓形式順時針轉動了2周,而一階力則沿著外面的橢圓順時針轉動了1周。
上面二階力的表現形式讓人們很容易聯想到:對于V型90°的機器,若兩列的往復質量相等,則二階往復慣性力的合力始終作用在水平線上,是一段經過圓心的線段。W型機器二階慣性力也有類似的性質,只不過將那線段從中間往上下拉,將線段變成了橢圓。對于上圖實際情形的質量分布,其二階力圖長半軸、短半軸為135.9N、46.8N,并且實際二階力圖是將上圖順轉了一個微小的角度。現將往復質量的不同更一般的情況列表如下:
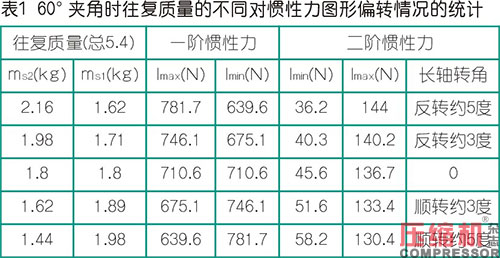
上表顯示了W型二級壓縮機,二級往復質量ms2偏離理論質量,會引起一階慣性力成橢圓變化。偏離越多橢圓化越嚴重,不論質量是增大還是減小;而其一周內的平均值始終不變。而二階慣性力則始終保持了長軸在水平方向,二級往復質量增大時,原長短徑3:1的橢圓愈扁平化,減小時愈圓形化。
對于上表第四欄,若將二級往復質量1.62增大,使總往復質量超出5.4千克,則會引起一、二階往復慣性力都增大。
2)按圖2形式作反時針轉動,其一、二階慣性力矢端力圖如圖5所示。
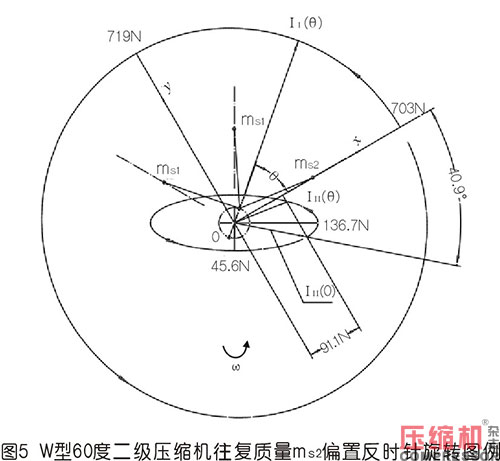
這里需說明的是,一階慣性力圖還是圖4種那個大橢圓,方向矢則順著曲柄矢沿軌跡圖反時針變化,兩矢量近似跟隨。二階慣性力圖也類似這樣,并且圖5與圖4起始的二階慣性力矢量IⅡ(0)不變。
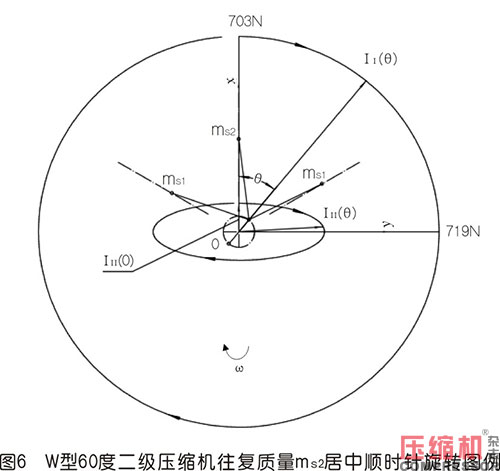
3)按圖3形式作順時針轉動,其一、二階慣性力矢端力圖如圖6所示。
應注意到對于往復質量固定的這些分布的型式,一、二階慣性力矢圖非常相似。也就是說,結構決定了力矢圖。文末再提及一下二階慣性力的橢圓應設法平衡,特別是在機器往大的方向發展時,往復質量ms、C值都變大時尤為需要。
〈本文未完待續,更多精彩內容見下期——〉
參考文獻
(1)宋瑞林,氣缸夾角為60°的V6車用發動機往復慣性力的平衡分析,[J],汽車技術,1988.8
(2)李松虎,3W型活塞壓縮機往復慣性力的分析,[J],壓縮機技術,1987.3
(3)陸鵬程,張光勝,三星型壓縮機振動問題研究,[J],安徽工程科技學院學報,2009.1
(4)王再順,夾角為90°的V型壓縮機往復慣性力平衡的探討,[J],壓縮機技術,1986.2
來源:本站原創
一、序言
【壓縮機網】W型壓縮機在我們的日常生活中非常常見。我廠目前已有的該類產品有0.5/14,0.9/10,1.25/10,1.8/8,CW480/40系列等。我們在這些年的生產和試制過程中發現:每種機器在初始試制中,由于三列的活塞等往復質量控制不理想,機器的設計轉速都在1000r/min左右,或許是剛開始設計活塞重量時欠考慮,機器試制時振動烈度都較高。隨著后期該種機器的批量投產,鋁活塞的質量也在強度允許范圍內有所下降,工程技術人員也意識到多級壓縮時不同級的活塞往復質量的偏差區間要從嚴考慮,現在W型機器的振動烈度比試制初期改善了許多。
本文以單曲拐、W型角度式壓縮機為例,由于往復質量的差異,從理論上分析推導出機器的一、二階往復慣性力的公式,該慣性力作用在曲軸箱體中心點上,該變化的慣性力的矢端在曲軸的運動平面上形成了慣性力的矢端軌跡力圖。根據該公式,提出合適的平衡一、二階往復慣性力的措施,用以推動國內的壓縮機的升級換代。
二、基礎理論
1.正方向的問題
W型壓縮機的三列連桿并列于同一的曲拐軸上,如圖1所示,為通用性計,該圖列之間夾角沒有畫成60°。我們這里考慮兩級壓縮機,它有兩個一級一個二級,設一級的往復部件質量為ms1,二級往復部件質量為ms2,以圖示的右邊的一列ms2為基準建立直角坐標系moy,規定投影到曲柄方向為x軸,與曲柄垂直的方向為y軸。這里規定x軸正方向是由機器中心向外指,這與壓縮機中將連桿受拉伸規定為正值相吻合,壓縮機動力計算時也將曲柄在上死點位置時運動部件受到的往復慣性力為正的最大值。y軸的正方向規定為將x軸順旋轉方向轉一直角方向為其正方向。這樣的規定都是為了方便計算,為后面的各種計算打下基礎,也更容易發現規律。
2.研究手段問題
本文采用歐拉公式研究三列慣性力矢量的合力問題,將教科書上推導過程中采用垂直和水平方向兩個式子合并成一個式子,這里規定x軸代表向量的實部,y軸代表向量的虛部,二者連接采用虛數單位i來連接。運用到的相關公式如下:
 (1)
(1)
 為工程指數,
為工程指數, 為虛數單位,
為虛數單位, 為曲柄轉角,單位為弧度,規定順時針旋轉方向為正值,θ為變量函數。該式子描述的也就是單位圓。
為曲柄轉角,單位為弧度,規定順時針旋轉方向為正值,θ為變量函數。該式子描述的也就是單位圓。
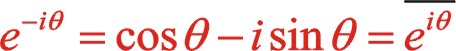 (2)
(2)
該式子也是上復數的共軛復數。

一階慣性力是余弦函數,本文將一對互為共軛的復數的平均值來研究一、二階慣性力。
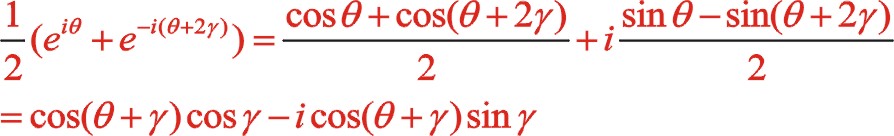 (4)
(4)
它巧妙地運用到兩個不同相位的歐拉函數的代數和來研究慣性力的投影問題。式子的右邊正好是圖示中中間列一階慣性力投影到xoy坐標系上兩個方向上兩個力的大小,根據前面規定了x,y軸的正方向,注意到上式的虛部應為負值。該式的“ ”用“—
”用“— ”代替后形成新的公式后文中也會運用到它。
”代替后形成新的公式后文中也會運用到它。
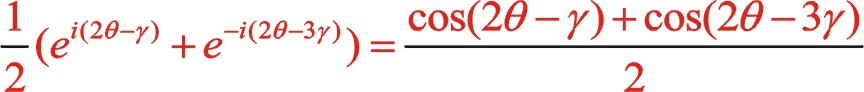
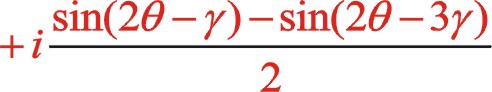
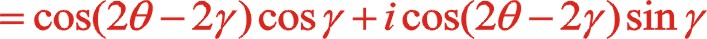 (5)
(5)
該式子是圖2中間列二階慣性力投影到xoy坐標系上兩個方向上兩個力的大小。該式的“ ![]() ”用“—
”用“— ![]() ”代替后形成新的公式就是圖1中二階慣性力的計算公式。
”代替后形成新的公式就是圖1中二階慣性力的計算公式。
3.研究切入點問題
本文研究慣性力的計算公式及其圖像,顧及三列不同的往復質量對計算公式的影響,所以研究的起始點非常重要。文章分析了兩種往復質量的計算公式,為計算方便,通常θ角的計入零點規定為ms2列活塞處于上死點的位置。文中得到的計算公式與選擇上面的計入零點無關。
三、計算過程
文中分析了ms2列活塞偏置一邊時順時針及反時針旋轉的一、二階往復慣性力的計算公式,對ms2列活塞置于中間時旋轉方向已不重要了,文中也分析了若順時針旋轉時計算公式。三列活塞套入曲柄銷的先后順序形成的慣性力矩也各不相同,由于微小,本文不作研究。文中假設三列都在同一個往復運動平面上往復慣性力合成后的矢端軌跡圖像。
1.用基礎理論分析圖1形式順時針轉動時慣性力

 (6)
(6)
r為曲柄半徑。ω為旋轉角速度,以弧度計入計算。C為后文列出的公式書寫方便引入的記號。
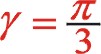
1.1一階慣性力的計算
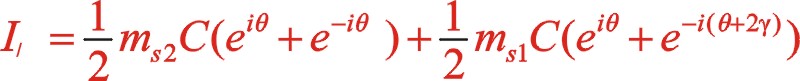
 (7)
(7)
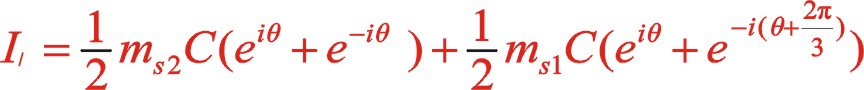
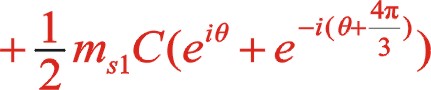

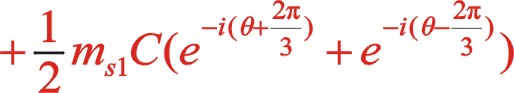
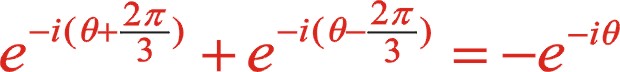
(8)
該式用到了三角函數的和差化積公式。
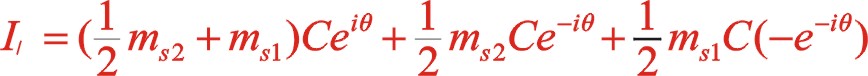
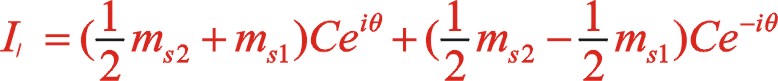
 (9)
(9)
上式就是W型夾角60°一階往復慣性力復數表達式。
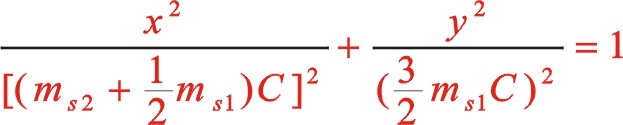 (10)
(10)
上式表明,一階慣性力矢端軌跡是一橢圓,變化的周期和曲軸旋轉的周期相同。該橢圓的圖像在運動平面上相當于將標準橢圓順時針旋轉了30°,若ms2>ms1,長半軸為(ms2+0.5ms1)C,短半軸為(1.5ms1)C;若ms2=ms1,橢圓退化成圓,半徑為(1.5ms1)C。
1.2二階慣性力的計算
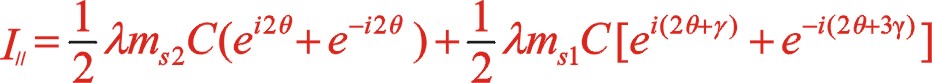
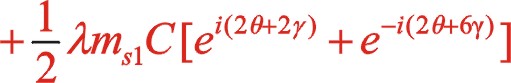 (11)
(11)
式中λ為曲柄半徑連桿比。
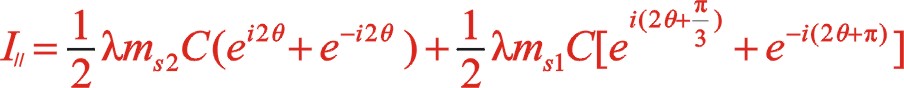
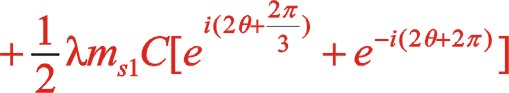

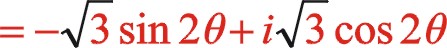 (12)
(12)
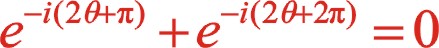 (13)
(13)
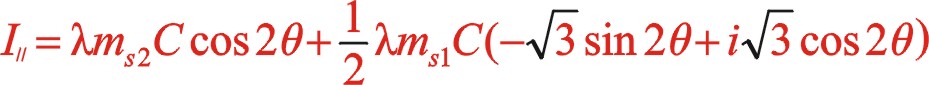
 (14)
(14)
這是W型夾角60°二階往復慣性力復數表達式。
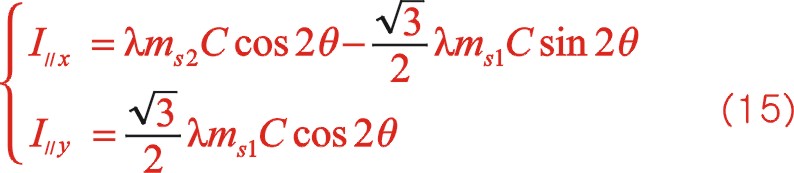
這也是二階慣性力參數方程的表達式。
為尋找上方程所描述的圖像,先假定兩個往復質量相等,利用尋找兩個變量的二次多項式方程方法和矩陣轉換法來進行。
 (16)
(16)
 (17)
(17)
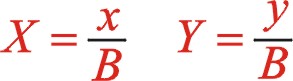
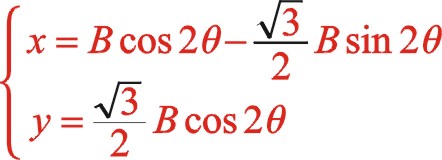
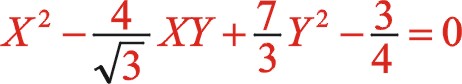 (18)
(18)
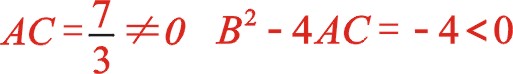
根據線性代數中二次多項式的判別式定理,滿足上兩個條件,所以二階慣性力也是一個橢圓。
坐標系順轉30°后,由于y軸在標準直角坐標的對面,相當于坐標系逆時針旋轉30°,作坐標系的矩陣變換的因子為
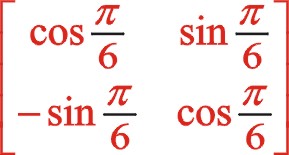

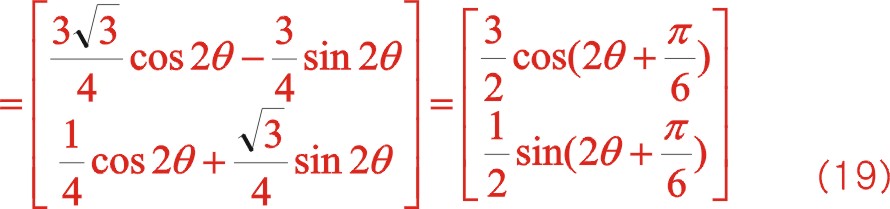
上式清晰地表明二階慣性力的軌跡是橢圓,變化的周期是曲軸旋轉的周期的一半。經坐標系的旋轉變換后的參數方程表明:該橢圓的長半軸是短半軸的3倍,不論是在xoy坐標系還是在x'oy'坐標系中,其橢圓的長半軸始終在水平方向,這與三列活塞在旋轉平面的分布緊密聯系,后文還分析表明,不論ms2處于偏置還是中間位置,不論旋轉方向,二階慣性力矢端力圖始終是橢圓,該橢圓的長軸始終處于水平方向,不過其相位變化比較復雜,式(19)可以看出θ為30°時,力矢到達該橢圓的短半軸位置,這兩個矢量不在同一方向成90°,θ為 — 15°時,力矢到達該橢圓的長半軸位置,這兩個矢量不在同一方向成45°。二階慣性力的變化比曲軸自身旋轉變化快一倍。
2.用基礎理論分析圖2形式反時針轉動時慣性力

2.2一階慣性力的計算
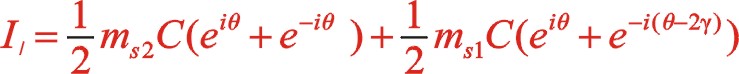
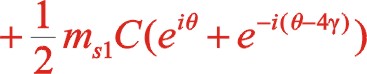 (20)
(20)
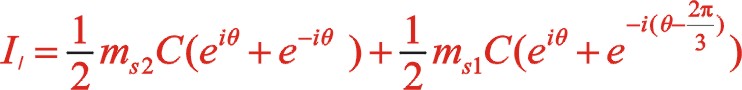
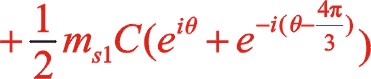
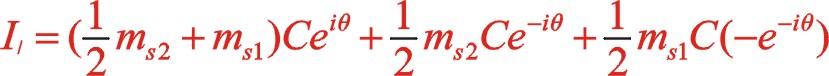
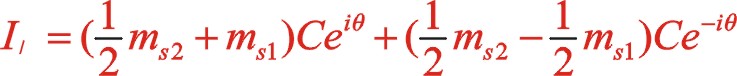

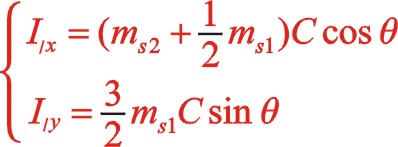
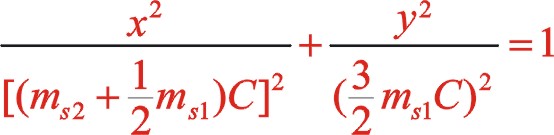
(21)
該式表明反時針旋轉時,一階慣性力復數方程和直角坐標方程形式上與順時針旋轉時完全相同,說明W型60°布置時,軌跡力圖與轉向無關,軌跡力矢的方向始終在曲柄轉動方向矢附近。當二者質量相等時,就成圓的變化,能夠在曲柄的反方向加一合適的平衡重,達到完全平衡掉一階往復慣性力。
2.2二階慣性力的計算
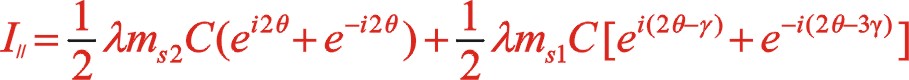
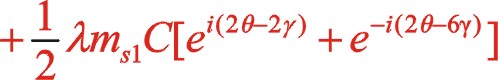 (22)
(22)
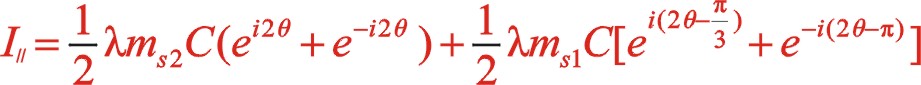
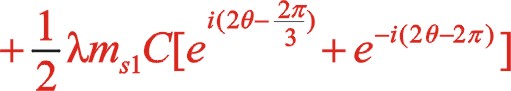
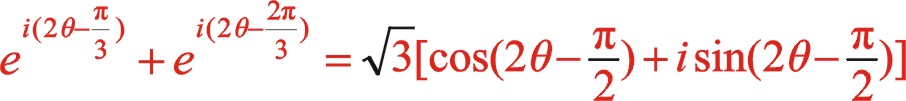
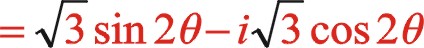




(23)
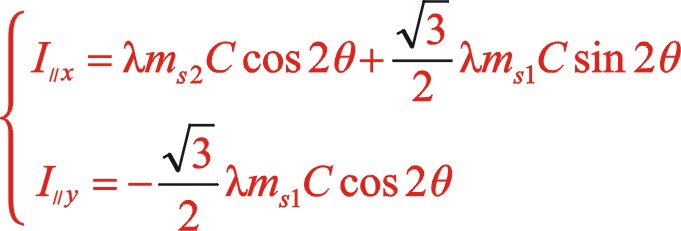
(24)
上式表明反時針旋轉時,二階慣性力直角坐標方程形式上與順時針旋轉時不同,說明換一個方向旋轉時,需要另一種方程描述二階慣性力的表現形式。后文的計算表明,它們的軌跡力圖是相同的。文章從理論提供了該力矢的數學表達式,希望能找到一種合適的機構加裝上也能夠平衡掉二階往復慣性力。
下面仿上面的假設,推導出它是一橢圓的依據。


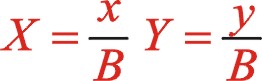
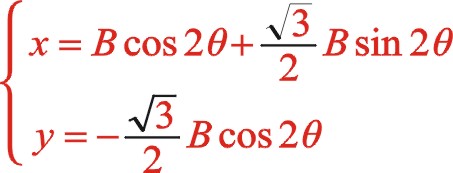
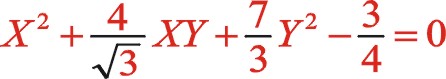
(25)
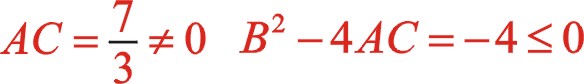
坐標系順轉30°后
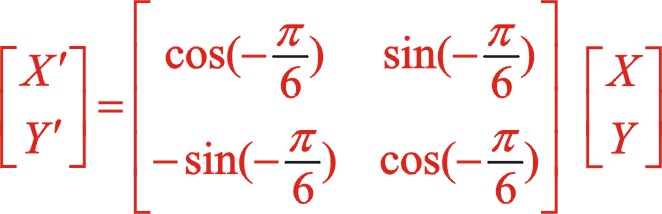
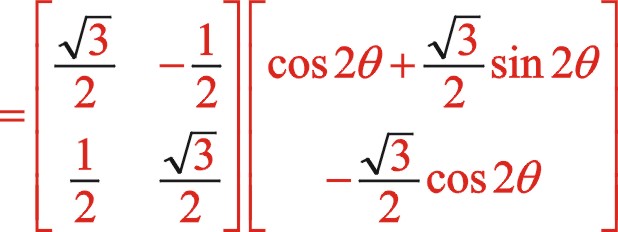
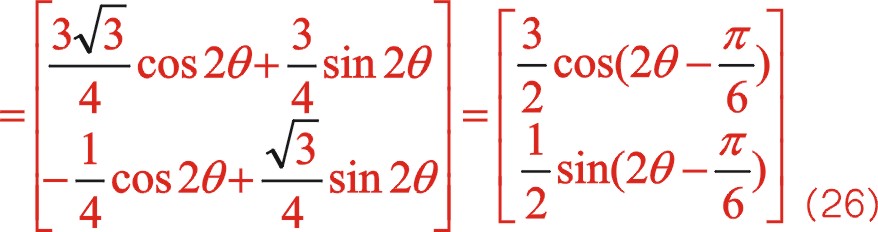
3.用基礎理論分析圖3形式順時針轉動時慣性力

3.1一階慣性力的計算
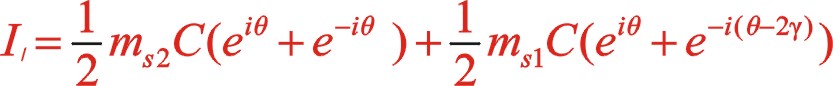
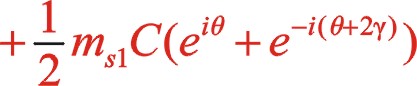
(27)
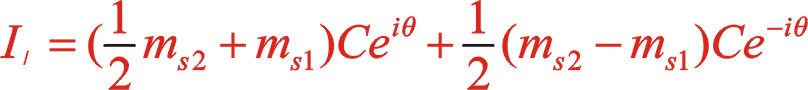

(28)
一階力矢成橢圓變化。
3.2二階慣性力的計算
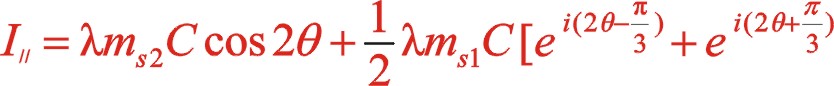
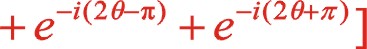
(29)
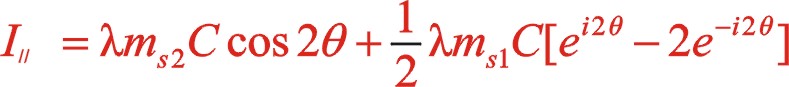

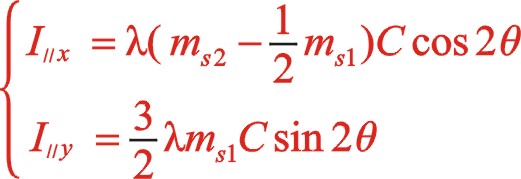
(30)
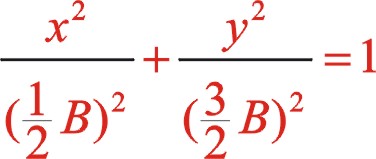
(31)
二階力矢也成橢圓變化,這種布置θ為0°時,力矢到達該橢圓的短半軸位置,曲柄方向矢與二階力矢在同一方向。
3.3討論
對于這種如圖3所示分布的機器,由式(28)、(30)可知:
①當ms2=ms1時,一階慣性力成圓的分布,二階慣性力成長短軸之比為3:1橢圓的分布;
②當ms2=2ms1時,一階慣性力成長短軸之比為5:3橢圓的分布,二階慣性力成圓的分布。
4.總結
從上面的三種情況分析和計算,可以得出W型60°布置有兩個ms1和一個ms2往復質量時有以下結論:
4.1一階慣性力是一橢圓,ms2列中心線是該橢圓的一個對稱軸方向,不論ms1、ms1、ms2在運動平面上如何分布,若ms2>ms1,則長軸在ms2列方向,反之則短軸在ms2列方向。
4.2二階慣性力也是一橢圓,若ms1=ms2,不論采用上面三種情況的特殊情形來計算,該橢圓的長軸始終在水平方向,短軸在豎直方向,并且長半軸是短半軸的3倍。若ms1≠ms2,則會將原來標準的橢圓作一適量旋轉,長短半軸的數值也會作微量變化。
四、舉例分析
本文以安徽華晶機械有限公司生產的WW-0.9/10B-Q型全無油空壓機為例分析W型60°二級壓縮機的一、二階往復慣性力。其中一級往復質量ms1為1.82kg,二級往復質量ms2為1.76kg,曲柄半徑為0.0375m,曲柄半徑連桿比λ為37.5/195,角速度ω為2π×(800/60)rad/s。現將上述結構參數分別代入上文中所列的相關公式中,運用計算機內EXCEL程序列表、繪圖計算分析,其結果如下:
1)按圖1形式作順時針轉動,其一、二階慣性力矢端力圖如圖4所示。

計算結果表明:當按照圖4所示建立的直角坐標系xoy后,按照順時針轉θ角后,一階往復慣性力如IⅠ(θ)所示,它是一個橢圓,二階往復慣性力如IⅡ(θ)所示,它也是一個很明顯的橢圓。一階慣性力的短半軸、長半軸為703N、719N,短軸在x軸方向上,該橢圓旋轉30°后形成標準橢圓。二階慣性力圖是按照總往復質量不變,三列往復質量相等繪制的(下同),即ms1=ms2=1.8kg,它是一個標準的橢圓,二階慣性力的長半軸、短半軸為136.7N、45.6N,長軸始終在水平方向,長短軸之比為3:1。圖中還顯示了當θ=0°,二階慣性力的向量是IⅡ(0),在x軸上刻度是91.1N,也就是式(11)中θ為0時的實部,該向量與x軸交角為40.9°,也就是說,初始的二階慣性力向量與曲柄矢不重合。當曲軸旋轉一周時,二階慣性力是從IⅡ(0)位置開始沿著其二階力橢圓形式順時針轉動了2周,而一階力則沿著外面的橢圓順時針轉動了1周。
上面二階力的表現形式讓人們很容易聯想到:對于V型90°的機器,若兩列的往復質量相等,則二階往復慣性力的合力始終作用在水平線上,是一段經過圓心的線段。W型機器二階慣性力也有類似的性質,只不過將那線段從中間往上下拉,將線段變成了橢圓。對于上圖實際情形的質量分布,其二階力圖長半軸、短半軸為135.9N、46.8N,并且實際二階力圖是將上圖順轉了一個微小的角度。現將往復質量的不同更一般的情況列表如下:

上表顯示了W型二級壓縮機,二級往復質量ms2偏離理論質量,會引起一階慣性力成橢圓變化。偏離越多橢圓化越嚴重,不論質量是增大還是減小;而其一周內的平均值始終不變。而二階慣性力則始終保持了長軸在水平方向,二級往復質量增大時,原長短徑3:1的橢圓愈扁平化,減小時愈圓形化。
對于上表第四欄,若將二級往復質量1.62增大,使總往復質量超出5.4千克,則會引起一、二階往復慣性力都增大。
2)按圖2形式作反時針轉動,其一、二階慣性力矢端力圖如圖5所示。

這里需說明的是,一階慣性力圖還是圖4種那個大橢圓,方向矢則順著曲柄矢沿軌跡圖反時針變化,兩矢量近似跟隨。二階慣性力圖也類似這樣,并且圖5與圖4起始的二階慣性力矢量IⅡ(0)不變。

3)按圖3形式作順時針轉動,其一、二階慣性力矢端力圖如圖6所示。
應注意到對于往復質量固定的這些分布的型式,一、二階慣性力矢圖非常相似。也就是說,結構決定了力矢圖。文末再提及一下二階慣性力的橢圓應設法平衡,特別是在機器往大的方向發展時,往復質量ms、C值都變大時尤為需要。
〈本文未完待續,更多精彩內容見下期——〉
參考文獻
(1)宋瑞林,氣缸夾角為60°的V6車用發動機往復慣性力的平衡分析,[J],汽車技術,1988.8
(2)李松虎,3W型活塞壓縮機往復慣性力的分析,[J],壓縮機技術,1987.3
(3)陸鵬程,張光勝,三星型壓縮機振動問題研究,[J],安徽工程科技學院學報,2009.1
(4)王再順,夾角為90°的V型壓縮機往復慣性力平衡的探討,[J],壓縮機技術,1986.2
來源:本站原創





網友評論
條評論
最新評論