【壓縮機(jī)網(wǎng)】隨著人工智能技術(shù)的快速發(fā)展,深度學(xué)習(xí)在各個(gè)領(lǐng)域的應(yīng)用也日趨廣泛。本文旨在探討AI深度學(xué)習(xí)在空壓系統(tǒng)策略優(yōu)化中的應(yīng)用,通過構(gòu)建深度學(xué)習(xí)模型,實(shí)現(xiàn)對(duì)空壓系統(tǒng)參數(shù)的精準(zhǔn)預(yù)測(cè)和優(yōu)化,以提高空壓系統(tǒng)的運(yùn)行效率。實(shí)驗(yàn)結(jié)果表明,對(duì)比機(jī)理模型和線性回歸模型,本文所提出的卷積神經(jīng)網(wǎng)絡(luò)建模的方法具有更好的模型訓(xùn)練效果,并結(jié)合遺傳算法為控制參數(shù)提供優(yōu)化,此方法為工業(yè)節(jié)能提供了新思路。
引言
隨著工業(yè)化進(jìn)程的加速和能源需求的不斷增長(zhǎng),空壓機(jī)作為工業(yè)領(lǐng)域的關(guān)鍵設(shè)備,其能耗問題日益凸顯。空壓機(jī)在各類工業(yè)生產(chǎn)過程中,如汽車、化工、電力、醫(yī)藥等,都發(fā)揮著至關(guān)重要的作用,但同時(shí)也是能源消耗的大戶。因此,如何降低空壓機(jī)的能耗,提高能源利用效率,已成為當(dāng)前工業(yè)節(jié)能領(lǐng)域亟待解決的問題[7]。
傳統(tǒng)的空壓機(jī)能耗優(yōu)化方法主要依賴于經(jīng)驗(yàn)調(diào)整或固定參數(shù)的優(yōu)化,雖然在一定程度上能夠降低能耗,但效果有限且難以適應(yīng)復(fù)雜多變的工業(yè)環(huán)境。
在空壓機(jī)深度學(xué)習(xí)建模應(yīng)用方面,研究者們已經(jīng)取得了一些初步的成果。通過模型預(yù)測(cè),可以實(shí)現(xiàn)對(duì)空壓機(jī)運(yùn)行狀態(tài)的實(shí)時(shí)監(jiān)測(cè)和預(yù)警,及時(shí)發(fā)現(xiàn)潛在故障,提高設(shè)備的可靠性和安全性[1][2][3][4][5]。還有一些研究者對(duì)空壓機(jī)用電需求規(guī)律進(jìn)行研究,利用長(zhǎng)短記憶模型(LSTM)取得了不錯(cuò)的結(jié)果[6]。也有研究者對(duì)燃?xì)廨啓C(jī)的多級(jí)壓縮機(jī)使用神經(jīng)網(wǎng)絡(luò)模型進(jìn)行建模[8],但對(duì)于用于工業(yè)場(chǎng)景的空壓機(jī)性能的建模以及優(yōu)化控制目前還較少有人研究。因此,研究一種新型的建模方法,實(shí)現(xiàn)對(duì)空壓系統(tǒng)的精準(zhǔn)控制和優(yōu)化,具有重要的現(xiàn)實(shí)意義和應(yīng)用價(jià)值。
一、建立深度學(xué)習(xí)空壓機(jī)模型
1.數(shù)據(jù)采集與預(yù)處理
在空壓機(jī)建模過程中,數(shù)據(jù)收集與處理是至關(guān)重要的一步。數(shù)據(jù)質(zhì)量直接影響到模型的準(zhǔn)確性和泛化能力。因此,我們對(duì)空壓機(jī)運(yùn)行數(shù)據(jù)進(jìn)行了細(xì)致的收集和處理工作。針對(duì)空壓機(jī)建模,將以下變量納入模型中:

在數(shù)據(jù)收集完成后,我們進(jìn)行了數(shù)據(jù)清洗工作,以去除異常值和重復(fù)數(shù)據(jù)。異常值可能是由于傳感器故障、數(shù)據(jù)傳輸錯(cuò)誤等原因產(chǎn)生的,它們會(huì)對(duì)模型的訓(xùn)練產(chǎn)生干擾,因此需要被識(shí)別并剔除。此處我們使用四分位法,并使用標(biāo)準(zhǔn)的1.5倍IQR值作為閾值,將超出正常范圍的數(shù)據(jù)標(biāo)記為異常值,并在后續(xù)的數(shù)據(jù)處理中將其排除。同時(shí)使用滑動(dòng)窗口濾波方法,以5個(gè)樣本作為窗口長(zhǎng)度,計(jì)算出滑動(dòng)平均值,對(duì)于超出平均值20%的原始樣本標(biāo)記為異常并在后續(xù)的處理中將其排除。重復(fù)數(shù)據(jù)則可能是由于數(shù)據(jù)采集系統(tǒng)的問題而產(chǎn)生的,我們需要去除這些冗余數(shù)據(jù),以避免對(duì)模型訓(xùn)練造成不必要的負(fù)擔(dān),此處我們對(duì)一組數(shù)據(jù)全部為重復(fù)的數(shù)據(jù)和空壓機(jī)功率數(shù)據(jù)重復(fù)的數(shù)據(jù)標(biāo)記為異常,并在后續(xù)的數(shù)據(jù)處理中將其排除。
2.多種方法建模對(duì)比
方法一:機(jī)理模型
機(jī)理模型使用如下公式

等價(jià)公式為
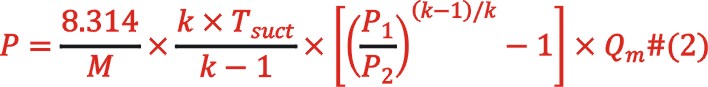
其中P壓縮機(jī)功率,對(duì)應(yīng)表格1中變量18;Tsuct空壓機(jī)進(jìn)口溫度(K),對(duì)比變量1;Tdischarge空壓機(jī)出口溫度(K),對(duì)應(yīng)變量14;M空氣摩爾質(zhì)量(g/mol)28.96;Qm空壓機(jī)流量(kg/s),對(duì)應(yīng)變量11;k空氣等熵系數(shù)1.4;P2空壓機(jī)出口壓力,對(duì)應(yīng)變量7;P1空壓機(jī)進(jìn)口壓力,對(duì)應(yīng)變量8。
方法二:線性回歸建模
線性回歸的目標(biāo)是找到一個(gè)最佳的直線(在多變量情況下是平面),使得這個(gè)直線(平面)與數(shù)據(jù)點(diǎn)之間的距離最小化[10]。這個(gè)距離通常是歐幾里得距離,即垂直距離。通過最小二乘法,可以求解線性回歸模型的參數(shù),從而實(shí)現(xiàn)連續(xù)型變量的預(yù)測(cè)。線性回歸模型可以表示為
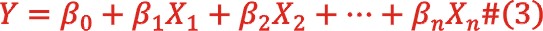
其中Y是因變量,X1,X2,...,Xn是自變量,β0,β1,β2,...,βn是模型的參數(shù)。本文中,將表格1中1-17號(hào)變量作為輸入,18號(hào)變量作為輸出,并使用最小二乘法求解出。
方法三:卷積神經(jīng)網(wǎng)絡(luò)建模
卷積神經(jīng)網(wǎng)絡(luò)(CNN)是一種專門用于處理具有網(wǎng)格結(jié)構(gòu)數(shù)據(jù)的神經(jīng)網(wǎng)絡(luò),如圖像數(shù)據(jù)。它通過卷積操作提取輸入數(shù)據(jù)的局部特征,并通過層次化的網(wǎng)絡(luò)結(jié)構(gòu)逐步抽象出更高級(jí)的特征表示。CNN在圖像識(shí)別、目標(biāo)檢測(cè)等領(lǐng)域取得了顯著的成功。CNN模型通常由卷積層、池化層、全連接層等組成。卷積層負(fù)責(zé)提取輸入數(shù)據(jù)的局部特征,通過卷積核與輸入數(shù)據(jù)的卷積運(yùn)算生成特征圖。池化層則負(fù)責(zé)對(duì)特征圖進(jìn)行下采樣,減少數(shù)據(jù)的維度和計(jì)算量,同時(shí)保留重要的特征信息。全連接層則負(fù)責(zé)將提取的特征映射到輸出空間,實(shí)現(xiàn)分類或回歸等任務(wù)[9]。
本文使用兩層3*1大小的卷積層,一層3*1大小的池化層,三層全連接層,每層之間均設(shè)置激活層,激活層均使用RELU函數(shù)。模型輸入為表格1中1-17號(hào)變量,模型輸出為18號(hào)變量。
3.建模結(jié)果對(duì)比
本次建模中,共對(duì)5臺(tái)空壓機(jī)進(jìn)行建模測(cè)試,對(duì)比上述3中建模方法,模型訓(xùn)練從3個(gè)指標(biāo)進(jìn)行評(píng)價(jià),分別是R2擬合系數(shù),R2定義式為
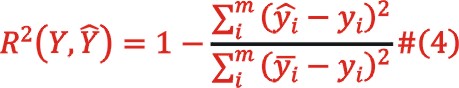
MAE平均絕對(duì)誤差,定義式為
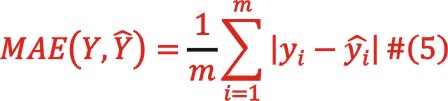
MAPE平均絕對(duì)誤差百分比,定義式為
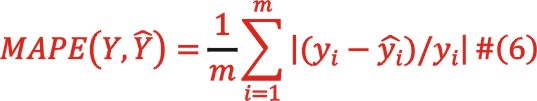
訓(xùn)練結(jié)果指標(biāo)如表2所示
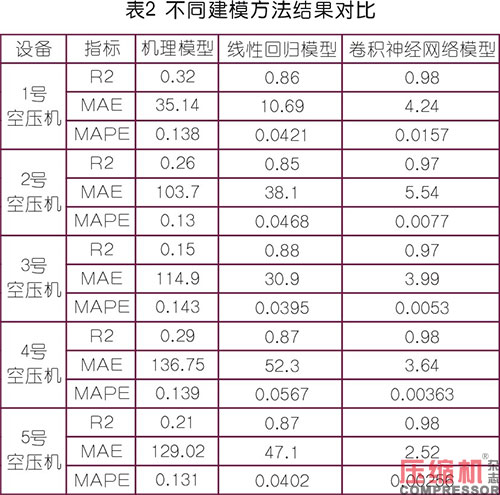
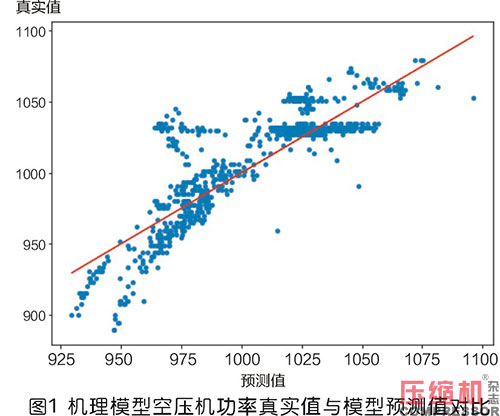
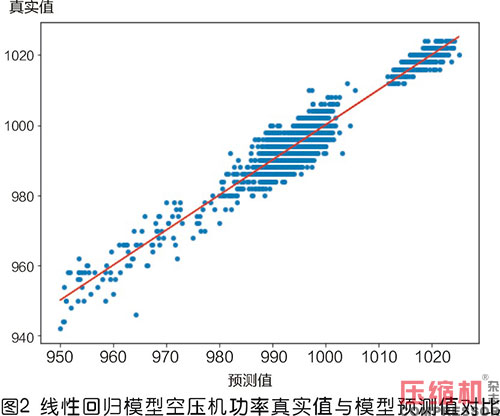
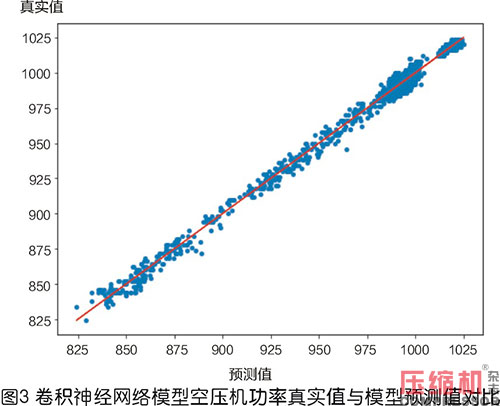
由表格2可以得知,CNN模型在5臺(tái)空壓機(jī)的建模中,在R2,MAE,MAPE這三個(gè)指標(biāo)中均取得了最佳的結(jié)果。同時(shí)根據(jù)圖1至圖3所示5號(hào)空壓機(jī)建模結(jié)果,機(jī)理建模方法僅對(duì)少量工況起到了較好的擬合效果,在900kW功率和1000kW功率附近均出現(xiàn)了較多的預(yù)測(cè)偏離樣本。線性回歸和CNN模型均有較好的擬合結(jié)果,但從模型指標(biāo)上看CNN模型的誤差更小。綜上所述,CNN網(wǎng)絡(luò)取得了最佳的訓(xùn)練效果,故使用此模型作為優(yōu)化的基礎(chǔ)。
二、優(yōu)化目標(biāo)及優(yōu)化算法選擇
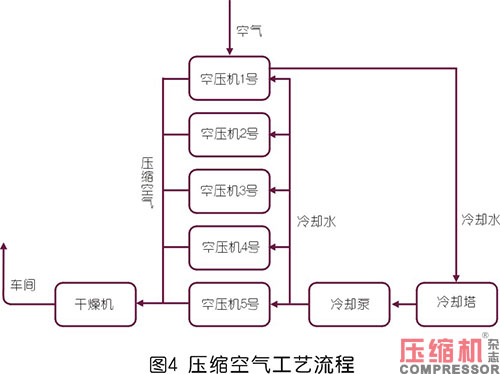
根據(jù)壓縮機(jī)變量特征和工藝流程分析,如圖4所示,空壓系統(tǒng)模型的輸入為每個(gè)空壓機(jī)模型輸入,輸出為5個(gè)空壓機(jī)模型輸出電功率之和,即

f1-f5為5臺(tái)空壓機(jī)模型,優(yōu)化目標(biāo)為公式(6)的總功率E最小,即空壓系統(tǒng)能耗最低。
遺傳算法(Genetic Algorithm,GA)是一種模擬自然選擇和遺傳機(jī)制的優(yōu)化算法。它借鑒了生物進(jìn)化過程中的自然選擇和遺傳學(xué)原理,通過模擬種群的進(jìn)化過程來(lái)搜索問題的最優(yōu)解。遺傳算法的基本思想是將問題的求解過程轉(zhuǎn)化為類似生物進(jìn)化中的染色體基因的交叉、變異等過程。在求解過程中,遺傳算法通過逐代進(jìn)化來(lái)搜索越來(lái)越好的近似解,每一代都根據(jù)問題域中個(gè)體的適應(yīng)度大小選擇個(gè)體,并借助于自然遺傳學(xué)的遺傳算子進(jìn)行組合交叉和變異,產(chǎn)生出代表新的解集的種群。這個(gè)過程將導(dǎo)致種群像自然進(jìn)化一樣的后生代種群,比前代更加適應(yīng)于環(huán)境,末代種群中的最優(yōu)個(gè)體經(jīng)過解碼,可以作為問題近似最優(yōu)解[11][12]。遺傳算法的基本步驟包括:
編碼:將問題的解空間轉(zhuǎn)化為遺傳算法能夠處理的搜索空間,即把問題的可能解從其解空間轉(zhuǎn)換到遺傳算法所能處理的搜索空間的轉(zhuǎn)換方法。
初始種群生成:隨機(jī)生成一組個(gè)體作為初始種群,這些個(gè)體代表問題的可能解。
適應(yīng)度評(píng)估:根據(jù)問題的目標(biāo)函數(shù),計(jì)算每個(gè)個(gè)體的適應(yīng)度值,評(píng)估其優(yōu)劣。
選擇:根據(jù)個(gè)體的適應(yīng)度值,選擇一部分優(yōu)秀個(gè)體進(jìn)入下一代,保證優(yōu)秀基因得以傳遞。
交叉(也稱雜交):將選擇出的個(gè)體進(jìn)行配對(duì),并按照一定的概率交換部分基因,生成新的個(gè)體。
變異:對(duì)交叉產(chǎn)生的個(gè)體按照一定的概率改變某些基因的值,以增加種群的多樣性。
終止條件判斷:若滿足終止條件(如達(dá)到最大迭代次數(shù)、找到滿意解等),則算法結(jié)束,輸出最優(yōu)解;否則,返回步驟3繼續(xù)迭代。
故使用遺傳算法對(duì)空壓系統(tǒng)模型的輸入?yún)?shù)進(jìn)行尋優(yōu),使得系統(tǒng)總功率最低的輸入?yún)?shù),即為最佳控制參數(shù)。本文中,使用表格1輸入變量中7空壓機(jī)出口壓力,11空壓機(jī)供氣流量,17空壓機(jī)開啟狀態(tài)最為可變量,其余輸入?yún)?shù)為固定常數(shù)取當(dāng)前實(shí)時(shí)值,變量18空壓機(jī)總功率作為尋優(yōu)目標(biāo),同時(shí)約束空壓系統(tǒng)總供氣流量在優(yōu)化后不能低于當(dāng)前實(shí)際值。種群個(gè)數(shù)設(shè)置為100,初始種群完全隨機(jī)生成,迭代次數(shù)為300次,無(wú)其它迭代停止條件。
三、算法驗(yàn)證
空壓機(jī)CNN模型訓(xùn)練完成后,使用兩個(gè)月的新數(shù)據(jù)對(duì)模型進(jìn)行測(cè)試,所有空壓機(jī)模型指標(biāo)MAE和MAPE均未超過模型訓(xùn)練時(shí)MAE和MAPE,測(cè)試集R2指標(biāo)不低于訓(xùn)練時(shí)R2,說(shuō)明CNN模型表現(xiàn)比較穩(wěn)定。
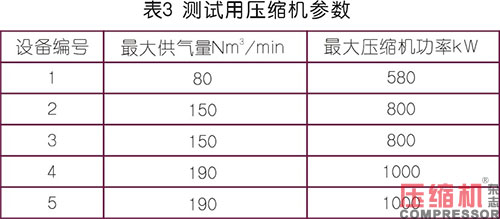
本文所提到的5臺(tái)空壓機(jī)參數(shù)如下表3:
我們將供氣需求量0-240帶入模型進(jìn)行優(yōu)化計(jì)算得到結(jié)果如下表4所示:
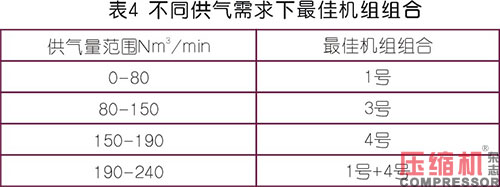
經(jīng)實(shí)際測(cè)試,在同樣的供氣量下CNN模型結(jié)合遺傳算法給出的最佳組合對(duì)比其它機(jī)組組合,具有更低的供氣能耗。
結(jié)論
本文嘗試了機(jī)理模型,線性回歸模型以及CNN模型,對(duì)比前兩種模型,CNN模型在模型精度上有優(yōu)勢(shì)。
CNN模型結(jié)合遺傳算法進(jìn)行空壓機(jī)控制參數(shù)優(yōu)化,可以找到最佳機(jī)組組合以及控制參數(shù),對(duì)比其它機(jī)組組合方式,此方法推理得到的機(jī)組組合整體能耗最低。
參考文獻(xiàn)
[1]王宇.基于數(shù)據(jù)驅(qū)動(dòng)的空壓機(jī)故障診斷與性能預(yù)測(cè)系統(tǒng)研究[D].上海應(yīng)用技術(shù)大學(xué),2021.
[2]馬玉寶,張興龍,李霖,等.基于數(shù)據(jù)驅(qū)動(dòng)的空壓機(jī)健康狀態(tài)評(píng)估[J].石油工程建設(shè),2023,49(1):62-66,87.DOI:10.3969/j.issn.1001-2206.2023.01.012.
[3]侯大立,王宇,成凡.基于數(shù)據(jù)驅(qū)動(dòng)的空壓機(jī)集群智能診斷系統(tǒng)[J].機(jī)床與液壓,2021,49(12):190-195.<br>HOU Dali,WANG Yu,CHENG Fan.Intelligent Diagnosis System of Air Compressor Cluster Based on Data driven[J].Machine Tool&Hydraulics,2021,49(12):190-195
[4]M.U.;Hameed,I.A.;Sundli,K.Health Monitoring of Air Compressors Using Reconstruction-Based Deep Learning for Anomaly Detection with Increased Transparency.Entropy 2021,23,83.https://doi.org/10.3390/e23010083
[5]胡歡歡.基于HHT和深度學(xué)習(xí)的船舶空壓機(jī)故障診斷[D].福建:集美大學(xué),2020.
[6]Da-Chun Wu,Babak Bahrami Asl,Ali Razban,Jie Chen,Air compressor load forecasting using artificial neural network,Expert Systems with Applications,Volume 168,2021,114209,ISSN 0957-4174,https://doi.org/10.1016/j.eswa.2020.114209.
[7]R.Saidur,N.A.Rahim,M.Hasanuzzaman,A review on compressed-air energy use and energy savings,Renewable and Sustainable Energy Reviews,Volume 14,Issue 4,2010,Pages 1135-1153,ISSN 1364-0321,https://doi.org/10.1016/j.rser.2009.11.013.
[8]K.Ghorbanian,M.Gholamrezaei,An artificial neural network approach to compressor performance prediction,Applied Energy,Volume 86,Issues 7 8,2009,Pages 1210-1221,ISSN 0306-2619,https://doi.org/10.1016/j.apenergy.2008.06.006.
[9]孫志軍,薛磊,許陽(yáng)明,等.深度學(xué)習(xí)研究綜述[J].計(jì)算機(jī)應(yīng)用研究,2012,29(8):5.DOI:10.3969/j.issn.1001-3695.2012.08.002.
[10]鄒樂強(qiáng).最小二乘法原理及其簡(jiǎn)單應(yīng)用[J].科技信息,2010(23):2.DOI:CNKI:SUN:KJXX.0.2010-23-209.
[11]周明,孫樹棟.遺傳算法原理及應(yīng)用[M].國(guó)防工業(yè)出版社,1999.
[12]丁建立,陳增強(qiáng),袁著祉.遺傳算法與螞蟻算法的融合[J].計(jì)算機(jī)研究與發(fā)展,2003,40(9):6.DOI:CNKI:SUN:JFYZ.0.2003-09-010.
來(lái)源:本站原創(chuàng)
【壓縮機(jī)網(wǎng)】隨著人工智能技術(shù)的快速發(fā)展,深度學(xué)習(xí)在各個(gè)領(lǐng)域的應(yīng)用也日趨廣泛。本文旨在探討AI深度學(xué)習(xí)在空壓系統(tǒng)策略優(yōu)化中的應(yīng)用,通過構(gòu)建深度學(xué)習(xí)模型,實(shí)現(xiàn)對(duì)空壓系統(tǒng)參數(shù)的精準(zhǔn)預(yù)測(cè)和優(yōu)化,以提高空壓系統(tǒng)的運(yùn)行效率。實(shí)驗(yàn)結(jié)果表明,對(duì)比機(jī)理模型和線性回歸模型,本文所提出的卷積神經(jīng)網(wǎng)絡(luò)建模的方法具有更好的模型訓(xùn)練效果,并結(jié)合遺傳算法為控制參數(shù)提供優(yōu)化,此方法為工業(yè)節(jié)能提供了新思路。
引言
隨著工業(yè)化進(jìn)程的加速和能源需求的不斷增長(zhǎng),空壓機(jī)作為工業(yè)領(lǐng)域的關(guān)鍵設(shè)備,其能耗問題日益凸顯。空壓機(jī)在各類工業(yè)生產(chǎn)過程中,如汽車、化工、電力、醫(yī)藥等,都發(fā)揮著至關(guān)重要的作用,但同時(shí)也是能源消耗的大戶。因此,如何降低空壓機(jī)的能耗,提高能源利用效率,已成為當(dāng)前工業(yè)節(jié)能領(lǐng)域亟待解決的問題[7]。
傳統(tǒng)的空壓機(jī)能耗優(yōu)化方法主要依賴于經(jīng)驗(yàn)調(diào)整或固定參數(shù)的優(yōu)化,雖然在一定程度上能夠降低能耗,但效果有限且難以適應(yīng)復(fù)雜多變的工業(yè)環(huán)境。
在空壓機(jī)深度學(xué)習(xí)建模應(yīng)用方面,研究者們已經(jīng)取得了一些初步的成果。通過模型預(yù)測(cè),可以實(shí)現(xiàn)對(duì)空壓機(jī)運(yùn)行狀態(tài)的實(shí)時(shí)監(jiān)測(cè)和預(yù)警,及時(shí)發(fā)現(xiàn)潛在故障,提高設(shè)備的可靠性和安全性[1][2][3][4][5]。還有一些研究者對(duì)空壓機(jī)用電需求規(guī)律進(jìn)行研究,利用長(zhǎng)短記憶模型(LSTM)取得了不錯(cuò)的結(jié)果[6]。也有研究者對(duì)燃?xì)廨啓C(jī)的多級(jí)壓縮機(jī)使用神經(jīng)網(wǎng)絡(luò)模型進(jìn)行建模[8],但對(duì)于用于工業(yè)場(chǎng)景的空壓機(jī)性能的建模以及優(yōu)化控制目前還較少有人研究。因此,研究一種新型的建模方法,實(shí)現(xiàn)對(duì)空壓系統(tǒng)的精準(zhǔn)控制和優(yōu)化,具有重要的現(xiàn)實(shí)意義和應(yīng)用價(jià)值。
一、建立深度學(xué)習(xí)空壓機(jī)模型
1.數(shù)據(jù)采集與預(yù)處理
在空壓機(jī)建模過程中,數(shù)據(jù)收集與處理是至關(guān)重要的一步。數(shù)據(jù)質(zhì)量直接影響到模型的準(zhǔn)確性和泛化能力。因此,我們對(duì)空壓機(jī)運(yùn)行數(shù)據(jù)進(jìn)行了細(xì)致的收集和處理工作。針對(duì)空壓機(jī)建模,將以下變量納入模型中:

在數(shù)據(jù)收集完成后,我們進(jìn)行了數(shù)據(jù)清洗工作,以去除異常值和重復(fù)數(shù)據(jù)。異常值可能是由于傳感器故障、數(shù)據(jù)傳輸錯(cuò)誤等原因產(chǎn)生的,它們會(huì)對(duì)模型的訓(xùn)練產(chǎn)生干擾,因此需要被識(shí)別并剔除。此處我們使用四分位法,并使用標(biāo)準(zhǔn)的1.5倍IQR值作為閾值,將超出正常范圍的數(shù)據(jù)標(biāo)記為異常值,并在后續(xù)的數(shù)據(jù)處理中將其排除。同時(shí)使用滑動(dòng)窗口濾波方法,以5個(gè)樣本作為窗口長(zhǎng)度,計(jì)算出滑動(dòng)平均值,對(duì)于超出平均值20%的原始樣本標(biāo)記為異常并在后續(xù)的處理中將其排除。重復(fù)數(shù)據(jù)則可能是由于數(shù)據(jù)采集系統(tǒng)的問題而產(chǎn)生的,我們需要去除這些冗余數(shù)據(jù),以避免對(duì)模型訓(xùn)練造成不必要的負(fù)擔(dān),此處我們對(duì)一組數(shù)據(jù)全部為重復(fù)的數(shù)據(jù)和空壓機(jī)功率數(shù)據(jù)重復(fù)的數(shù)據(jù)標(biāo)記為異常,并在后續(xù)的數(shù)據(jù)處理中將其排除。
2.多種方法建模對(duì)比
方法一:機(jī)理模型
機(jī)理模型使用如下公式

等價(jià)公式為
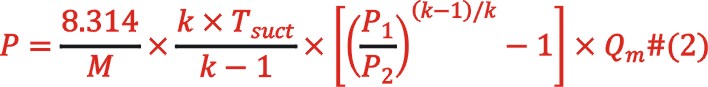
其中P壓縮機(jī)功率,對(duì)應(yīng)表格1中變量18;Tsuct空壓機(jī)進(jìn)口溫度(K),對(duì)比變量1;Tdischarge空壓機(jī)出口溫度(K),對(duì)應(yīng)變量14;M空氣摩爾質(zhì)量(g/mol)28.96;Qm空壓機(jī)流量(kg/s),對(duì)應(yīng)變量11;k空氣等熵系數(shù)1.4;P2空壓機(jī)出口壓力,對(duì)應(yīng)變量7;P1空壓機(jī)進(jìn)口壓力,對(duì)應(yīng)變量8。
方法二:線性回歸建模
線性回歸的目標(biāo)是找到一個(gè)最佳的直線(在多變量情況下是平面),使得這個(gè)直線(平面)與數(shù)據(jù)點(diǎn)之間的距離最小化[10]。這個(gè)距離通常是歐幾里得距離,即垂直距離。通過最小二乘法,可以求解線性回歸模型的參數(shù),從而實(shí)現(xiàn)連續(xù)型變量的預(yù)測(cè)。線性回歸模型可以表示為
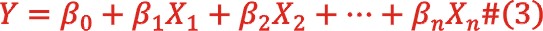
其中Y是因變量,X1,X2,...,Xn是自變量,β0,β1,β2,...,βn是模型的參數(shù)。本文中,將表格1中1-17號(hào)變量作為輸入,18號(hào)變量作為輸出,并使用最小二乘法求解出。
方法三:卷積神經(jīng)網(wǎng)絡(luò)建模
卷積神經(jīng)網(wǎng)絡(luò)(CNN)是一種專門用于處理具有網(wǎng)格結(jié)構(gòu)數(shù)據(jù)的神經(jīng)網(wǎng)絡(luò),如圖像數(shù)據(jù)。它通過卷積操作提取輸入數(shù)據(jù)的局部特征,并通過層次化的網(wǎng)絡(luò)結(jié)構(gòu)逐步抽象出更高級(jí)的特征表示。CNN在圖像識(shí)別、目標(biāo)檢測(cè)等領(lǐng)域取得了顯著的成功。CNN模型通常由卷積層、池化層、全連接層等組成。卷積層負(fù)責(zé)提取輸入數(shù)據(jù)的局部特征,通過卷積核與輸入數(shù)據(jù)的卷積運(yùn)算生成特征圖。池化層則負(fù)責(zé)對(duì)特征圖進(jìn)行下采樣,減少數(shù)據(jù)的維度和計(jì)算量,同時(shí)保留重要的特征信息。全連接層則負(fù)責(zé)將提取的特征映射到輸出空間,實(shí)現(xiàn)分類或回歸等任務(wù)[9]。
本文使用兩層3*1大小的卷積層,一層3*1大小的池化層,三層全連接層,每層之間均設(shè)置激活層,激活層均使用RELU函數(shù)。模型輸入為表格1中1-17號(hào)變量,模型輸出為18號(hào)變量。
3.建模結(jié)果對(duì)比
本次建模中,共對(duì)5臺(tái)空壓機(jī)進(jìn)行建模測(cè)試,對(duì)比上述3中建模方法,模型訓(xùn)練從3個(gè)指標(biāo)進(jìn)行評(píng)價(jià),分別是R2擬合系數(shù),R2定義式為
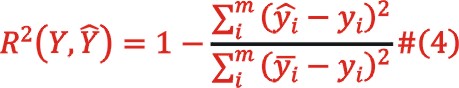
MAE平均絕對(duì)誤差,定義式為
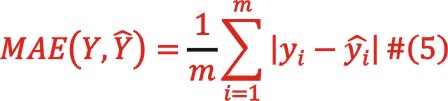
MAPE平均絕對(duì)誤差百分比,定義式為
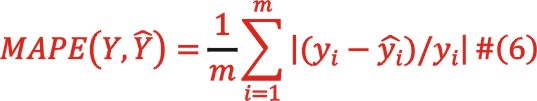
訓(xùn)練結(jié)果指標(biāo)如表2所示




由表格2可以得知,CNN模型在5臺(tái)空壓機(jī)的建模中,在R2,MAE,MAPE這三個(gè)指標(biāo)中均取得了最佳的結(jié)果。同時(shí)根據(jù)圖1至圖3所示5號(hào)空壓機(jī)建模結(jié)果,機(jī)理建模方法僅對(duì)少量工況起到了較好的擬合效果,在900kW功率和1000kW功率附近均出現(xiàn)了較多的預(yù)測(cè)偏離樣本。線性回歸和CNN模型均有較好的擬合結(jié)果,但從模型指標(biāo)上看CNN模型的誤差更小。綜上所述,CNN網(wǎng)絡(luò)取得了最佳的訓(xùn)練效果,故使用此模型作為優(yōu)化的基礎(chǔ)。
二、優(yōu)化目標(biāo)及優(yōu)化算法選擇

根據(jù)壓縮機(jī)變量特征和工藝流程分析,如圖4所示,空壓系統(tǒng)模型的輸入為每個(gè)空壓機(jī)模型輸入,輸出為5個(gè)空壓機(jī)模型輸出電功率之和,即

f1-f5為5臺(tái)空壓機(jī)模型,優(yōu)化目標(biāo)為公式(6)的總功率E最小,即空壓系統(tǒng)能耗最低。
遺傳算法(Genetic Algorithm,GA)是一種模擬自然選擇和遺傳機(jī)制的優(yōu)化算法。它借鑒了生物進(jìn)化過程中的自然選擇和遺傳學(xué)原理,通過模擬種群的進(jìn)化過程來(lái)搜索問題的最優(yōu)解。遺傳算法的基本思想是將問題的求解過程轉(zhuǎn)化為類似生物進(jìn)化中的染色體基因的交叉、變異等過程。在求解過程中,遺傳算法通過逐代進(jìn)化來(lái)搜索越來(lái)越好的近似解,每一代都根據(jù)問題域中個(gè)體的適應(yīng)度大小選擇個(gè)體,并借助于自然遺傳學(xué)的遺傳算子進(jìn)行組合交叉和變異,產(chǎn)生出代表新的解集的種群。這個(gè)過程將導(dǎo)致種群像自然進(jìn)化一樣的后生代種群,比前代更加適應(yīng)于環(huán)境,末代種群中的最優(yōu)個(gè)體經(jīng)過解碼,可以作為問題近似最優(yōu)解[11][12]。遺傳算法的基本步驟包括:
編碼:將問題的解空間轉(zhuǎn)化為遺傳算法能夠處理的搜索空間,即把問題的可能解從其解空間轉(zhuǎn)換到遺傳算法所能處理的搜索空間的轉(zhuǎn)換方法。
初始種群生成:隨機(jī)生成一組個(gè)體作為初始種群,這些個(gè)體代表問題的可能解。
適應(yīng)度評(píng)估:根據(jù)問題的目標(biāo)函數(shù),計(jì)算每個(gè)個(gè)體的適應(yīng)度值,評(píng)估其優(yōu)劣。
選擇:根據(jù)個(gè)體的適應(yīng)度值,選擇一部分優(yōu)秀個(gè)體進(jìn)入下一代,保證優(yōu)秀基因得以傳遞。
交叉(也稱雜交):將選擇出的個(gè)體進(jìn)行配對(duì),并按照一定的概率交換部分基因,生成新的個(gè)體。
變異:對(duì)交叉產(chǎn)生的個(gè)體按照一定的概率改變某些基因的值,以增加種群的多樣性。
終止條件判斷:若滿足終止條件(如達(dá)到最大迭代次數(shù)、找到滿意解等),則算法結(jié)束,輸出最優(yōu)解;否則,返回步驟3繼續(xù)迭代。
故使用遺傳算法對(duì)空壓系統(tǒng)模型的輸入?yún)?shù)進(jìn)行尋優(yōu),使得系統(tǒng)總功率最低的輸入?yún)?shù),即為最佳控制參數(shù)。本文中,使用表格1輸入變量中7空壓機(jī)出口壓力,11空壓機(jī)供氣流量,17空壓機(jī)開啟狀態(tài)最為可變量,其余輸入?yún)?shù)為固定常數(shù)取當(dāng)前實(shí)時(shí)值,變量18空壓機(jī)總功率作為尋優(yōu)目標(biāo),同時(shí)約束空壓系統(tǒng)總供氣流量在優(yōu)化后不能低于當(dāng)前實(shí)際值。種群個(gè)數(shù)設(shè)置為100,初始種群完全隨機(jī)生成,迭代次數(shù)為300次,無(wú)其它迭代停止條件。
三、算法驗(yàn)證
空壓機(jī)CNN模型訓(xùn)練完成后,使用兩個(gè)月的新數(shù)據(jù)對(duì)模型進(jìn)行測(cè)試,所有空壓機(jī)模型指標(biāo)MAE和MAPE均未超過模型訓(xùn)練時(shí)MAE和MAPE,測(cè)試集R2指標(biāo)不低于訓(xùn)練時(shí)R2,說(shuō)明CNN模型表現(xiàn)比較穩(wěn)定。
本文所提到的5臺(tái)空壓機(jī)參數(shù)如下表3:

我們將供氣需求量0-240帶入模型進(jìn)行優(yōu)化計(jì)算得到結(jié)果如下表4所示:

經(jīng)實(shí)際測(cè)試,在同樣的供氣量下CNN模型結(jié)合遺傳算法給出的最佳組合對(duì)比其它機(jī)組組合,具有更低的供氣能耗。
結(jié)論
本文嘗試了機(jī)理模型,線性回歸模型以及CNN模型,對(duì)比前兩種模型,CNN模型在模型精度上有優(yōu)勢(shì)。
CNN模型結(jié)合遺傳算法進(jìn)行空壓機(jī)控制參數(shù)優(yōu)化,可以找到最佳機(jī)組組合以及控制參數(shù),對(duì)比其它機(jī)組組合方式,此方法推理得到的機(jī)組組合整體能耗最低。
參考文獻(xiàn)
[1]王宇.基于數(shù)據(jù)驅(qū)動(dòng)的空壓機(jī)故障診斷與性能預(yù)測(cè)系統(tǒng)研究[D].上海應(yīng)用技術(shù)大學(xué),2021.
[2]馬玉寶,張興龍,李霖,等.基于數(shù)據(jù)驅(qū)動(dòng)的空壓機(jī)健康狀態(tài)評(píng)估[J].石油工程建設(shè),2023,49(1):62-66,87.DOI:10.3969/j.issn.1001-2206.2023.01.012.
[3]侯大立,王宇,成凡.基于數(shù)據(jù)驅(qū)動(dòng)的空壓機(jī)集群智能診斷系統(tǒng)[J].機(jī)床與液壓,2021,49(12):190-195.<br>HOU Dali,WANG Yu,CHENG Fan.Intelligent Diagnosis System of Air Compressor Cluster Based on Data driven[J].Machine Tool&Hydraulics,2021,49(12):190-195
[4]M.U.;Hameed,I.A.;Sundli,K.Health Monitoring of Air Compressors Using Reconstruction-Based Deep Learning for Anomaly Detection with Increased Transparency.Entropy 2021,23,83.https://doi.org/10.3390/e23010083
[5]胡歡歡.基于HHT和深度學(xué)習(xí)的船舶空壓機(jī)故障診斷[D].福建:集美大學(xué),2020.
[6]Da-Chun Wu,Babak Bahrami Asl,Ali Razban,Jie Chen,Air compressor load forecasting using artificial neural network,Expert Systems with Applications,Volume 168,2021,114209,ISSN 0957-4174,https://doi.org/10.1016/j.eswa.2020.114209.
[7]R.Saidur,N.A.Rahim,M.Hasanuzzaman,A review on compressed-air energy use and energy savings,Renewable and Sustainable Energy Reviews,Volume 14,Issue 4,2010,Pages 1135-1153,ISSN 1364-0321,https://doi.org/10.1016/j.rser.2009.11.013.
[8]K.Ghorbanian,M.Gholamrezaei,An artificial neural network approach to compressor performance prediction,Applied Energy,Volume 86,Issues 7 8,2009,Pages 1210-1221,ISSN 0306-2619,https://doi.org/10.1016/j.apenergy.2008.06.006.
[9]孫志軍,薛磊,許陽(yáng)明,等.深度學(xué)習(xí)研究綜述[J].計(jì)算機(jī)應(yīng)用研究,2012,29(8):5.DOI:10.3969/j.issn.1001-3695.2012.08.002.
[10]鄒樂強(qiáng).最小二乘法原理及其簡(jiǎn)單應(yīng)用[J].科技信息,2010(23):2.DOI:CNKI:SUN:KJXX.0.2010-23-209.
[11]周明,孫樹棟.遺傳算法原理及應(yīng)用[M].國(guó)防工業(yè)出版社,1999.
[12]丁建立,陳增強(qiáng),袁著祉.遺傳算法與螞蟻算法的融合[J].計(jì)算機(jī)研究與發(fā)展,2003,40(9):6.DOI:CNKI:SUN:JFYZ.0.2003-09-010.
來(lái)源:本站原創(chuàng)











網(wǎng)友評(píng)論
條評(píng)論
最新評(píng)論