【壓縮機(jī)網(wǎng)】在2023年10月刊《準(zhǔn)雙作用式壓縮機(jī)理論問題研究》一文中,筆者推導(dǎo)了準(zhǔn)雙作用式壓縮機(jī)的活塞位移公式,介紹了其在壓縮機(jī)研究、設(shè)計(jì)中的應(yīng)用,并提到了壓縮機(jī)動(dòng)力計(jì)算。本文在探討壓縮機(jī)動(dòng)力計(jì)算程序之前,先具體談?wù)剺?gòu)成壓縮機(jī)活塞力成分之一——慣性力的問題。
1、慣性力概念發(fā)展簡(jiǎn)史
先簡(jiǎn)單談?wù)剛鹘y(tǒng)的手工繪制動(dòng)力曲線的計(jì)算方法。構(gòu)成列的活塞力由氣體力、慣性力、摩擦力三部分相加之和而形成。列的氣體力圖采用勃?jiǎng)诙颍˙rauer)法繪制;列的慣性力圖通常采用托爾(Tolle)法繪制,近似地繪制出一階、二階慣性力之和;列的摩擦力圖是按經(jīng)驗(yàn)法繪制,通常的做法是在向軸行程中認(rèn)為是一不變的正值,而在向蓋行程中則認(rèn)為是一負(fù)的不變的值,在內(nèi)、外止點(diǎn)時(shí)作一斜線修正。它的作用方向始終與活塞運(yùn)動(dòng)速度方向相反。這三種方法繪制的各自力圖中,都面臨著橫坐標(biāo)的轉(zhuǎn)換,因?yàn)榛钊綁嚎s機(jī)是曲柄連桿機(jī)構(gòu),將主運(yùn)動(dòng)的旋轉(zhuǎn)運(yùn)動(dòng)通過連桿轉(zhuǎn)換成活塞的上、下往復(fù)運(yùn)動(dòng)。各自的力圖一般先采用“力-位移”坐標(biāo)系,它們都是周期性的,主曲柄旋轉(zhuǎn)一周360°時(shí),活塞則經(jīng)“外止點(diǎn)-內(nèi)止點(diǎn)-外止點(diǎn)”這樣一個(gè)循環(huán)。而列的活塞力圖一般采用“力-曲柄轉(zhuǎn)角”坐標(biāo)系構(gòu)成,包括后來的列的切向力圖、列的法向力圖、列的連桿力圖、列的側(cè)向力圖,都是采用這樣的坐標(biāo)系來分析。所以說,對(duì)于橫坐標(biāo)由行程轉(zhuǎn)化為曲柄旋轉(zhuǎn)角的問題,教材上都給出了采用勃力克斯(Brix)近似作圖法,并給予了相應(yīng)證明,這里不作展開論述。這就是傳統(tǒng)的手工作圖方法,而現(xiàn)在則直接采用經(jīng)推導(dǎo)的公式將三種力圖直接繪制成“力-曲柄轉(zhuǎn)角”坐標(biāo)系中。不過有些細(xì)節(jié)仍是近似的。例如,氣體力經(jīng)氣閥的作用,在轉(zhuǎn)折點(diǎn)處沒有考慮現(xiàn)實(shí)中的脈動(dòng)狀態(tài),慣性力圖也僅考慮了一、二階,對(duì)其后的三階等沒有考慮,而摩擦力圖是最簡(jiǎn)單的簡(jiǎn)化過程,并且統(tǒng)計(jì)出的機(jī)械效率具體值也是一個(gè)經(jīng)驗(yàn)值。雖然是這樣但這些簡(jiǎn)化也是我們動(dòng)力計(jì)算時(shí)作出的正確抉擇。
慣性力是什么?歷史上關(guān)于慣性力的爭(zhēng)論由來已久,可追溯到三百年前左右。慣性力就是按達(dá)朗伯原理,將動(dòng)力學(xué)問題轉(zhuǎn)化成靜力學(xué)問題的一種研究方法。這種力比較特殊,它沒有明確的力的三要素概念,所以有些人認(rèn)為是虛擬的,它實(shí)際上是以“-ma”形式出現(xiàn)。而更多的學(xué)者堅(jiān)持認(rèn)為它是一種真實(shí)的力,不然就無法解釋高速旋轉(zhuǎn)的機(jī)器,例如航空燃?xì)鉁u輪葉片根部斷裂現(xiàn)象。這些在壓縮機(jī)上也有類似的現(xiàn)象,歸根到底都是實(shí)際物體的內(nèi)力與外力、相對(duì)與絕對(duì)的問題。
2、壓縮機(jī)中慣性力的大小
據(jù)作者統(tǒng)計(jì),在各種型式的壓縮機(jī)中,構(gòu)成某一列的活塞運(yùn)動(dòng)組件,其該列受到的往復(fù)慣性力的幅值占該列所受到的氣體力的幅值百分比,約為7~40%,這是作者不完全的統(tǒng)計(jì)。它基于作者目前所了解到的各種國內(nèi)的壓縮機(jī)經(jīng)作者近似比算的,實(shí)際反映了各型的設(shè)計(jì)者對(duì)慣性力的認(rèn)識(shí)作出的設(shè)計(jì)。請(qǐng)讀者應(yīng)該注意的是,這里的活塞包括單作用式、雙作用式的,而這里的慣性力的演算方法則是該篇文章所詳細(xì)討論的內(nèi)容。


其中:Imax——列的最大往復(fù)慣性力
ms——蓋側(cè)往復(fù)質(zhì)量,包括蓋側(cè)活塞、環(huán)、活塞桿、十字頭體、銷、連桿重心偏向于小頭部分的連桿質(zhì)量(約占連桿總質(zhì)量的30~40%),kg。軸側(cè)質(zhì)量待后面討論
r——曲柄半徑,m
ω——曲柄旋轉(zhuǎn)角速度,1/s,,n為機(jī)器轉(zhuǎn)速,r/min
λ——曲柄半徑連桿中心距之比,,為連桿中心距長(zhǎng)度


其中:δd2——準(zhǔn)雙作用式蓋側(cè)容積腔部分的排氣時(shí)相對(duì)壓力損失
Pd2——準(zhǔn)雙作用式蓋側(cè)容積腔部分的名義的排氣絕對(duì)壓力,bar
Fh2——該容積腔所作用的活塞面積,m2,

代表蓋側(cè)氣缸直徑

其中:P平——指平衡腔的壓力,bar,它與機(jī)器的運(yùn)動(dòng)機(jī)構(gòu)利用系數(shù)μ有關(guān)。一般接一級(jí)排壓力腔,它可以減輕高壓缸活塞環(huán)工作負(fù)荷,避免向低壓級(jí)腔泄漏,這里計(jì)算B值時(shí)不考慮。
Fh氣缸圓環(huán)——指下面的大氣缸與上面的小氣缸工作面積差,m2

其中:δs1——準(zhǔn)雙作用式軸側(cè)容積腔部分的吸氣時(shí)相對(duì)壓力損失
Ps1——準(zhǔn)雙作用式軸側(cè)容積腔部分的名義的吸氣絕對(duì)壓力,bar
Fh1——該容積腔所作用的活塞面積,m2,

代表軸側(cè)氣缸直徑,d代表活塞桿直徑
Pgas——列的最大氣體力,它一般指的是蓋側(cè)活塞θ=0而軸側(cè)活塞處在θ=π時(shí)的狀態(tài)
B——慣性力的幅值與氣體力的幅值的百分比,%
3、關(guān)于慣性力在準(zhǔn)雙作用式壓縮機(jī)中表現(xiàn)形式的幾種思考
大家知道,在曲柄連桿機(jī)構(gòu)中,列的往復(fù)慣性力I為:
注意,它通常指的是蓋側(cè)活塞的慣性力。相信大部分讀者可能都比較迷惑,為什么剛開始作慣性力圖時(shí),在外止點(diǎn)即θ=0時(shí),將作在正力方向時(shí),就能將上式“-”取消?這是因?yàn)椋谏w側(cè)活塞工作過程中,θ=0°開始后,位移由0漸變正(方向向下),速度也是由0漸變正(方向向下),而加速度則是由正的最大值漸變小(引起的速度還是漸變大),其方向也是向下,加個(gè)負(fù)號(hào)則方向變上,則此時(shí)該力的作用使連桿受拉,故手工作圖時(shí)作在正力方向上,已考慮了“-”。
同理,θ=180°時(shí),,該值為負(fù),作在“力-曲柄轉(zhuǎn)角”坐標(biāo)系下方。
下面以具有圖1形式的準(zhǔn)雙作用式壓縮機(jī)某一列為算例,詳盡討論對(duì)變值的慣性力計(jì)算的思考。

已知:活塞組件質(zhì)量7.8kg(其上小活塞3.2kg,下面大活塞4.6kg)
環(huán)0.6kg
活塞桿8.2kg
十字頭10kg
銷1.4kg
連桿小頭4kg
綜上,運(yùn)動(dòng)部件總質(zhì)量32kg,其中蓋側(cè)運(yùn)動(dòng)部件總質(zhì)量27.4kg,軸側(cè)運(yùn)動(dòng)部件總質(zhì)量28.8kg
曲柄旋轉(zhuǎn)半徑

角速度

曲柄半徑連桿比

觀點(diǎn)一:僅考慮了蓋側(cè)活塞組件的質(zhì)量
由(7)式得到:


由此得到慣性力的最大值與最小值為11.13,-7.95kN。以該數(shù)系同氣體力、摩擦力參與了該列活塞力的演算,忽略了軸側(cè)大活塞的影響,可能當(dāng)時(shí)還沒有意識(shí)到軸側(cè)慣性力如何計(jì)算。
觀點(diǎn)二:因?yàn)榘凑談?dòng)力的傳遞,由連桿小頭帶動(dòng)十字頭、活塞桿,進(jìn)而大活塞、小活塞,作上下往復(fù)運(yùn)動(dòng),認(rèn)為:




由此得到慣性力的最大值與最小值為0.41,-0.57kN。其中第二項(xiàng)是這樣演算的:當(dāng)將內(nèi)止點(diǎn)選做坐標(biāo)系的原點(diǎn),向上為正方向,以軸側(cè)活塞開始膨脹點(diǎn)為起始點(diǎn)后,其:




當(dāng)蓋側(cè)與軸側(cè)都統(tǒng)一到蓋側(cè)的外止點(diǎn)處一套坐標(biāo)系后,也考慮到初始時(shí)各自的正負(fù)值后,總的慣性力應(yīng)是蓋側(cè)的慣性力與式(10)的之和(不過后來發(fā)現(xiàn)還是不對(duì)),大家可能發(fā)現(xiàn)蓋側(cè)與軸側(cè)往復(fù)質(zhì)量中將連桿小頭、十字頭、活塞桿質(zhì)量計(jì)及了兩次,算出的參與計(jì)算的質(zhì)量?jī)H是大、小活塞質(zhì)量的差值,這不知有沒有道理?不過我們或許都知道,慣性力在機(jī)器運(yùn)轉(zhuǎn)過程中,不參與做功,不影響最終平均切向力的大小,僅影響活塞力和平均切向力的具體形狀,影響機(jī)器曲軸的靜強(qiáng)度計(jì)算,并且其幅值相對(duì)氣體力來說較小。
觀點(diǎn)三:由觀點(diǎn)二得出推論, 、計(jì)入可能有誤,應(yīng)該是
、計(jì)入可能有誤,應(yīng)該是 ,所以。
,所以。
觀點(diǎn)四:不論以蓋側(cè)活塞計(jì)算慣性力的變化曲線,還是以軸側(cè)活塞來計(jì)算,其計(jì)算結(jié)果都是一樣的,即以觀點(diǎn)一中的公式來計(jì)算,式中ms=32kg,證明如下:


由此得到慣性力的最大值與最小值為13,-9.29kN。
根據(jù)蓋側(cè)的位移、速度、加速度圖解,見圖2。



據(jù)軸側(cè)的位移、速度、加速度圖解,見圖3。它就是按式(8)、(9)、(10)分兩部分疊加而成。
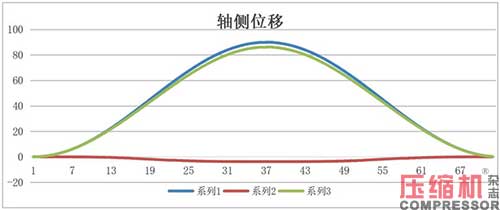


軸側(cè)0°時(shí),位移為正(方向向上),速度為正(向上),加速度為正(向上),-ma向下,連桿受壓,作在負(fù)值(-1+λ)處;軸側(cè)180°時(shí),位移為正的最大值,速度為0漸變負(fù)(向下),加速度為負(fù)的最大值(向下),-ma向上,連桿受拉,作在正值(1+λ)處。
由此可見,形式上具有圖1中的大活塞進(jìn)行的軸側(cè)加速度的變化,其受力分析表明,在統(tǒng)一的一套坐標(biāo)系中θ=0時(shí),將慣性力的起始點(diǎn)作在正的(1+λ)為力的系數(shù)處,參與的質(zhì)量是全部的往復(fù)運(yùn)動(dòng)質(zhì)量,這正好與普通蓋側(cè)慣性力曲線起始點(diǎn)作圖一致。這很好地解決了觀點(diǎn)二和觀點(diǎn)三中十字頭等處質(zhì)量參與計(jì)算兩次的問題,當(dāng)時(shí)也因?yàn)檫@一處質(zhì)量通過大活塞又給了小活塞感到困惑、十分不解。對(duì)于這種準(zhǔn)雙作用式或者就是雙作用式活塞,描述的位移公式形式上有兩種,經(jīng)求導(dǎo)后得出的加速度公式也有兩種,然而形成的慣性力表現(xiàn)形式僅有一種,正好等同于傳統(tǒng)的單作用式的那種,這些都是經(jīng)過嚴(yán)密推導(dǎo)出來的,不是主觀臆測(cè)的。科學(xué)是十分奇妙的,講究對(duì)稱與嚴(yán)謹(jǐn),當(dāng)你深入下去就會(huì)探索到“山窮水復(fù)疑無路,柳暗花明又一村”的境界。將軸側(cè)加速度圖與蓋側(cè)加速度圖相對(duì)照,軸側(cè)180°開始后再添個(gè)負(fù)號(hào),就是蓋側(cè)的加速度線。
壓縮機(jī)教材上指出,實(shí)際上制作慣性力曲線時(shí),是直接作在各列氣體力曲線一起的,以便與摩擦力一道疊加成活塞力曲線。根據(jù)動(dòng)力計(jì)算程序得出,具有觀點(diǎn)四形成的慣性力曲線與觀點(diǎn)一、二、三相比較,合成后的總活塞力的72組數(shù)據(jù)中的最大值居最小,雖然各自相差不多。
點(diǎn)評(píng):以上四種觀點(diǎn)層層推進(jìn),步步為營,最終得出了觀點(diǎn)四的正確結(jié)論。觀點(diǎn)一抓大放小,它與觀點(diǎn)四在各個(gè)位置時(shí)力的分析都是相差最小的,雖然看起來有些粗糙;觀點(diǎn)二的毛病,從后面來看是沒有考慮到軸側(cè)活塞的慣性力對(duì)連桿的作用受壓還是受拉,即觀點(diǎn)二式I后是以“-”來連接,同時(shí)重復(fù)計(jì)及十字頭等往復(fù)質(zhì)量,所以不對(duì);觀點(diǎn)三認(rèn)同兩質(zhì)量相等是一大進(jìn)步,若 、取兩項(xiàng)相加就多算了一份;觀點(diǎn)四是正確的結(jié)論,它是觀點(diǎn)一、二、三的完美概括。
、取兩項(xiàng)相加就多算了一份;觀點(diǎn)四是正確的結(jié)論,它是觀點(diǎn)一、二、三的完美概括。
4、準(zhǔn)雙作用活塞組件θ=45°時(shí)受力分析
最后以統(tǒng)一坐標(biāo)系中,θ約45°分析一下活塞的受力,見圖4。

說明一下,F(xiàn)g1、Fg2、Fg平、Ff1、Ff2、I、N、Fl組成一組平衡力系,圖中每一種力的箭頭標(biāo)示了該狀態(tài)下的方向。用Fp表示活塞力,則其表達(dá)式為:
參考文獻(xiàn)
(1)陳永江,容積式壓縮機(jī)原理與結(jié)構(gòu)設(shè)計(jì),[M],西安交通大學(xué)出版,1985
(2)林梅,孫嗣瑩,活塞式壓縮機(jī)原理,[M],西安交通大學(xué),2006
(3)陸鵬程,張光勝,三星型壓縮機(jī)振動(dòng)問題研究,[J],安徽工程科技學(xué)院學(xué)報(bào),2009.1:62-65
(4)侯寶安,關(guān)于慣性力的看法,[J],山東建材學(xué)院學(xué)報(bào),1987.1
(5)張玉良,上海化學(xué)工業(yè)專科學(xué)校,慣性力辨析,化工裝備技術(shù),1989.10
來源:本站原創(chuàng)
【壓縮機(jī)網(wǎng)】在2023年10月刊《準(zhǔn)雙作用式壓縮機(jī)理論問題研究》一文中,筆者推導(dǎo)了準(zhǔn)雙作用式壓縮機(jī)的活塞位移公式,介紹了其在壓縮機(jī)研究、設(shè)計(jì)中的應(yīng)用,并提到了壓縮機(jī)動(dòng)力計(jì)算。本文在探討壓縮機(jī)動(dòng)力計(jì)算程序之前,先具體談?wù)剺?gòu)成壓縮機(jī)活塞力成分之一——慣性力的問題。
1、慣性力概念發(fā)展簡(jiǎn)史
先簡(jiǎn)單談?wù)剛鹘y(tǒng)的手工繪制動(dòng)力曲線的計(jì)算方法。構(gòu)成列的活塞力由氣體力、慣性力、摩擦力三部分相加之和而形成。列的氣體力圖采用勃?jiǎng)诙颍˙rauer)法繪制;列的慣性力圖通常采用托爾(Tolle)法繪制,近似地繪制出一階、二階慣性力之和;列的摩擦力圖是按經(jīng)驗(yàn)法繪制,通常的做法是在向軸行程中認(rèn)為是一不變的正值,而在向蓋行程中則認(rèn)為是一負(fù)的不變的值,在內(nèi)、外止點(diǎn)時(shí)作一斜線修正。它的作用方向始終與活塞運(yùn)動(dòng)速度方向相反。這三種方法繪制的各自力圖中,都面臨著橫坐標(biāo)的轉(zhuǎn)換,因?yàn)榛钊綁嚎s機(jī)是曲柄連桿機(jī)構(gòu),將主運(yùn)動(dòng)的旋轉(zhuǎn)運(yùn)動(dòng)通過連桿轉(zhuǎn)換成活塞的上、下往復(fù)運(yùn)動(dòng)。各自的力圖一般先采用“力-位移”坐標(biāo)系,它們都是周期性的,主曲柄旋轉(zhuǎn)一周360°時(shí),活塞則經(jīng)“外止點(diǎn)-內(nèi)止點(diǎn)-外止點(diǎn)”這樣一個(gè)循環(huán)。而列的活塞力圖一般采用“力-曲柄轉(zhuǎn)角”坐標(biāo)系構(gòu)成,包括后來的列的切向力圖、列的法向力圖、列的連桿力圖、列的側(cè)向力圖,都是采用這樣的坐標(biāo)系來分析。所以說,對(duì)于橫坐標(biāo)由行程轉(zhuǎn)化為曲柄旋轉(zhuǎn)角的問題,教材上都給出了采用勃力克斯(Brix)近似作圖法,并給予了相應(yīng)證明,這里不作展開論述。這就是傳統(tǒng)的手工作圖方法,而現(xiàn)在則直接采用經(jīng)推導(dǎo)的公式將三種力圖直接繪制成“力-曲柄轉(zhuǎn)角”坐標(biāo)系中。不過有些細(xì)節(jié)仍是近似的。例如,氣體力經(jīng)氣閥的作用,在轉(zhuǎn)折點(diǎn)處沒有考慮現(xiàn)實(shí)中的脈動(dòng)狀態(tài),慣性力圖也僅考慮了一、二階,對(duì)其后的三階等沒有考慮,而摩擦力圖是最簡(jiǎn)單的簡(jiǎn)化過程,并且統(tǒng)計(jì)出的機(jī)械效率具體值也是一個(gè)經(jīng)驗(yàn)值。雖然是這樣但這些簡(jiǎn)化也是我們動(dòng)力計(jì)算時(shí)作出的正確抉擇。
慣性力是什么?歷史上關(guān)于慣性力的爭(zhēng)論由來已久,可追溯到三百年前左右。慣性力就是按達(dá)朗伯原理,將動(dòng)力學(xué)問題轉(zhuǎn)化成靜力學(xué)問題的一種研究方法。這種力比較特殊,它沒有明確的力的三要素概念,所以有些人認(rèn)為是虛擬的,它實(shí)際上是以“-ma”形式出現(xiàn)。而更多的學(xué)者堅(jiān)持認(rèn)為它是一種真實(shí)的力,不然就無法解釋高速旋轉(zhuǎn)的機(jī)器,例如航空燃?xì)鉁u輪葉片根部斷裂現(xiàn)象。這些在壓縮機(jī)上也有類似的現(xiàn)象,歸根到底都是實(shí)際物體的內(nèi)力與外力、相對(duì)與絕對(duì)的問題。
2、壓縮機(jī)中慣性力的大小
據(jù)作者統(tǒng)計(jì),在各種型式的壓縮機(jī)中,構(gòu)成某一列的活塞運(yùn)動(dòng)組件,其該列受到的往復(fù)慣性力的幅值占該列所受到的氣體力的幅值百分比,約為7~40%,這是作者不完全的統(tǒng)計(jì)。它基于作者目前所了解到的各種國內(nèi)的壓縮機(jī)經(jīng)作者近似比算的,實(shí)際反映了各型的設(shè)計(jì)者對(duì)慣性力的認(rèn)識(shí)作出的設(shè)計(jì)。請(qǐng)讀者應(yīng)該注意的是,這里的活塞包括單作用式、雙作用式的,而這里的慣性力的演算方法則是該篇文章所詳細(xì)討論的內(nèi)容。


其中:Imax——列的最大往復(fù)慣性力
ms——蓋側(cè)往復(fù)質(zhì)量,包括蓋側(cè)活塞、環(huán)、活塞桿、十字頭體、銷、連桿重心偏向于小頭部分的連桿質(zhì)量(約占連桿總質(zhì)量的30~40%),kg。軸側(cè)質(zhì)量待后面討論
r——曲柄半徑,m
ω——曲柄旋轉(zhuǎn)角速度,1/s,,n為機(jī)器轉(zhuǎn)速,r/min
λ——曲柄半徑連桿中心距之比,,為連桿中心距長(zhǎng)度


其中:δd2——準(zhǔn)雙作用式蓋側(cè)容積腔部分的排氣時(shí)相對(duì)壓力損失
Pd2——準(zhǔn)雙作用式蓋側(cè)容積腔部分的名義的排氣絕對(duì)壓力,bar
Fh2——該容積腔所作用的活塞面積,m2,

代表蓋側(cè)氣缸直徑

其中:P平——指平衡腔的壓力,bar,它與機(jī)器的運(yùn)動(dòng)機(jī)構(gòu)利用系數(shù)μ有關(guān)。一般接一級(jí)排壓力腔,它可以減輕高壓缸活塞環(huán)工作負(fù)荷,避免向低壓級(jí)腔泄漏,這里計(jì)算B值時(shí)不考慮。
Fh氣缸圓環(huán)——指下面的大氣缸與上面的小氣缸工作面積差,m2

其中:δs1——準(zhǔn)雙作用式軸側(cè)容積腔部分的吸氣時(shí)相對(duì)壓力損失
Ps1——準(zhǔn)雙作用式軸側(cè)容積腔部分的名義的吸氣絕對(duì)壓力,bar
Fh1——該容積腔所作用的活塞面積,m2,

代表軸側(cè)氣缸直徑,d代表活塞桿直徑
Pgas——列的最大氣體力,它一般指的是蓋側(cè)活塞θ=0而軸側(cè)活塞處在θ=π時(shí)的狀態(tài)
B——慣性力的幅值與氣體力的幅值的百分比,%
3、關(guān)于慣性力在準(zhǔn)雙作用式壓縮機(jī)中表現(xiàn)形式的幾種思考
大家知道,在曲柄連桿機(jī)構(gòu)中,列的往復(fù)慣性力I為:
注意,它通常指的是蓋側(cè)活塞的慣性力。相信大部分讀者可能都比較迷惑,為什么剛開始作慣性力圖時(shí),在外止點(diǎn)即θ=0時(shí),將作在正力方向時(shí),就能將上式“-”取消?這是因?yàn)椋谏w側(cè)活塞工作過程中,θ=0°開始后,位移由0漸變正(方向向下),速度也是由0漸變正(方向向下),而加速度則是由正的最大值漸變小(引起的速度還是漸變大),其方向也是向下,加個(gè)負(fù)號(hào)則方向變上,則此時(shí)該力的作用使連桿受拉,故手工作圖時(shí)作在正力方向上,已考慮了“-”。
同理,θ=180°時(shí),,該值為負(fù),作在“力-曲柄轉(zhuǎn)角”坐標(biāo)系下方。
下面以具有圖1形式的準(zhǔn)雙作用式壓縮機(jī)某一列為算例,詳盡討論對(duì)變值的慣性力計(jì)算的思考。

已知:活塞組件質(zhì)量7.8kg(其上小活塞3.2kg,下面大活塞4.6kg)
環(huán)0.6kg
活塞桿8.2kg
十字頭10kg
銷1.4kg
連桿小頭4kg
綜上,運(yùn)動(dòng)部件總質(zhì)量32kg,其中蓋側(cè)運(yùn)動(dòng)部件總質(zhì)量27.4kg,軸側(cè)運(yùn)動(dòng)部件總質(zhì)量28.8kg
曲柄旋轉(zhuǎn)半徑

角速度

曲柄半徑連桿比

觀點(diǎn)一:僅考慮了蓋側(cè)活塞組件的質(zhì)量
由(7)式得到:


由此得到慣性力的最大值與最小值為11.13,-7.95kN。以該數(shù)系同氣體力、摩擦力參與了該列活塞力的演算,忽略了軸側(cè)大活塞的影響,可能當(dāng)時(shí)還沒有意識(shí)到軸側(cè)慣性力如何計(jì)算。
觀點(diǎn)二:因?yàn)榘凑談?dòng)力的傳遞,由連桿小頭帶動(dòng)十字頭、活塞桿,進(jìn)而大活塞、小活塞,作上下往復(fù)運(yùn)動(dòng),認(rèn)為:




由此得到慣性力的最大值與最小值為0.41,-0.57kN。其中第二項(xiàng)是這樣演算的:當(dāng)將內(nèi)止點(diǎn)選做坐標(biāo)系的原點(diǎn),向上為正方向,以軸側(cè)活塞開始膨脹點(diǎn)為起始點(diǎn)后,其:




當(dāng)蓋側(cè)與軸側(cè)都統(tǒng)一到蓋側(cè)的外止點(diǎn)處一套坐標(biāo)系后,也考慮到初始時(shí)各自的正負(fù)值后,總的慣性力應(yīng)是蓋側(cè)的慣性力與式(10)的之和(不過后來發(fā)現(xiàn)還是不對(duì)),大家可能發(fā)現(xiàn)蓋側(cè)與軸側(cè)往復(fù)質(zhì)量中將連桿小頭、十字頭、活塞桿質(zhì)量計(jì)及了兩次,算出的參與計(jì)算的質(zhì)量?jī)H是大、小活塞質(zhì)量的差值,這不知有沒有道理?不過我們或許都知道,慣性力在機(jī)器運(yùn)轉(zhuǎn)過程中,不參與做功,不影響最終平均切向力的大小,僅影響活塞力和平均切向力的具體形狀,影響機(jī)器曲軸的靜強(qiáng)度計(jì)算,并且其幅值相對(duì)氣體力來說較小。
觀點(diǎn)三:由觀點(diǎn)二得出推論, 、計(jì)入可能有誤,應(yīng)該是
、計(jì)入可能有誤,應(yīng)該是 ,所以。
,所以。
觀點(diǎn)四:不論以蓋側(cè)活塞計(jì)算慣性力的變化曲線,還是以軸側(cè)活塞來計(jì)算,其計(jì)算結(jié)果都是一樣的,即以觀點(diǎn)一中的公式來計(jì)算,式中ms=32kg,證明如下:


由此得到慣性力的最大值與最小值為13,-9.29kN。
根據(jù)蓋側(cè)的位移、速度、加速度圖解,見圖2。



據(jù)軸側(cè)的位移、速度、加速度圖解,見圖3。它就是按式(8)、(9)、(10)分兩部分疊加而成。



軸側(cè)0°時(shí),位移為正(方向向上),速度為正(向上),加速度為正(向上),-ma向下,連桿受壓,作在負(fù)值(-1+λ)處;軸側(cè)180°時(shí),位移為正的最大值,速度為0漸變負(fù)(向下),加速度為負(fù)的最大值(向下),-ma向上,連桿受拉,作在正值(1+λ)處。
由此可見,形式上具有圖1中的大活塞進(jìn)行的軸側(cè)加速度的變化,其受力分析表明,在統(tǒng)一的一套坐標(biāo)系中θ=0時(shí),將慣性力的起始點(diǎn)作在正的(1+λ)為力的系數(shù)處,參與的質(zhì)量是全部的往復(fù)運(yùn)動(dòng)質(zhì)量,這正好與普通蓋側(cè)慣性力曲線起始點(diǎn)作圖一致。這很好地解決了觀點(diǎn)二和觀點(diǎn)三中十字頭等處質(zhì)量參與計(jì)算兩次的問題,當(dāng)時(shí)也因?yàn)檫@一處質(zhì)量通過大活塞又給了小活塞感到困惑、十分不解。對(duì)于這種準(zhǔn)雙作用式或者就是雙作用式活塞,描述的位移公式形式上有兩種,經(jīng)求導(dǎo)后得出的加速度公式也有兩種,然而形成的慣性力表現(xiàn)形式僅有一種,正好等同于傳統(tǒng)的單作用式的那種,這些都是經(jīng)過嚴(yán)密推導(dǎo)出來的,不是主觀臆測(cè)的。科學(xué)是十分奇妙的,講究對(duì)稱與嚴(yán)謹(jǐn),當(dāng)你深入下去就會(huì)探索到“山窮水復(fù)疑無路,柳暗花明又一村”的境界。將軸側(cè)加速度圖與蓋側(cè)加速度圖相對(duì)照,軸側(cè)180°開始后再添個(gè)負(fù)號(hào),就是蓋側(cè)的加速度線。
壓縮機(jī)教材上指出,實(shí)際上制作慣性力曲線時(shí),是直接作在各列氣體力曲線一起的,以便與摩擦力一道疊加成活塞力曲線。根據(jù)動(dòng)力計(jì)算程序得出,具有觀點(diǎn)四形成的慣性力曲線與觀點(diǎn)一、二、三相比較,合成后的總活塞力的72組數(shù)據(jù)中的最大值居最小,雖然各自相差不多。
點(diǎn)評(píng):以上四種觀點(diǎn)層層推進(jìn),步步為營,最終得出了觀點(diǎn)四的正確結(jié)論。觀點(diǎn)一抓大放小,它與觀點(diǎn)四在各個(gè)位置時(shí)力的分析都是相差最小的,雖然看起來有些粗糙;觀點(diǎn)二的毛病,從后面來看是沒有考慮到軸側(cè)活塞的慣性力對(duì)連桿的作用受壓還是受拉,即觀點(diǎn)二式I后是以“-”來連接,同時(shí)重復(fù)計(jì)及十字頭等往復(fù)質(zhì)量,所以不對(duì);觀點(diǎn)三認(rèn)同兩質(zhì)量相等是一大進(jìn)步,若 、取兩項(xiàng)相加就多算了一份;觀點(diǎn)四是正確的結(jié)論,它是觀點(diǎn)一、二、三的完美概括。
、取兩項(xiàng)相加就多算了一份;觀點(diǎn)四是正確的結(jié)論,它是觀點(diǎn)一、二、三的完美概括。
4、準(zhǔn)雙作用活塞組件θ=45°時(shí)受力分析
最后以統(tǒng)一坐標(biāo)系中,θ約45°分析一下活塞的受力,見圖4。

說明一下,F(xiàn)g1、Fg2、Fg平、Ff1、Ff2、I、N、Fl組成一組平衡力系,圖中每一種力的箭頭標(biāo)示了該狀態(tài)下的方向。用Fp表示活塞力,則其表達(dá)式為:
參考文獻(xiàn)
(1)陳永江,容積式壓縮機(jī)原理與結(jié)構(gòu)設(shè)計(jì),[M],西安交通大學(xué)出版,1985
(2)林梅,孫嗣瑩,活塞式壓縮機(jī)原理,[M],西安交通大學(xué),2006
(3)陸鵬程,張光勝,三星型壓縮機(jī)振動(dòng)問題研究,[J],安徽工程科技學(xué)院學(xué)報(bào),2009.1:62-65
(4)侯寶安,關(guān)于慣性力的看法,[J],山東建材學(xué)院學(xué)報(bào),1987.1
(5)張玉良,上海化學(xué)工業(yè)專科學(xué)校,慣性力辨析,化工裝備技術(shù),1989.10
來源:本站原創(chuàng)











網(wǎng)友評(píng)論
條評(píng)論
最新評(píng)論