【壓縮機網】編者按:空壓機作為一種通用動力機械設備,涉及到很多方面的知識,比如流體力學、電學、
材料學、機械設計等等。而熱力學就屬于極為重要的一部分,從業者不可不知。本文將對空壓機中涉及到的熱力學相關知識進行分享,希望對大家起到參考作用。
1.基本定律
熱力學第一基礎定律是一個自然界的規律,無法證明,但卻為人們義無反顧地所接受。它既不能被創造也不會被消滅。熱力學第二規律說:熱是永遠無法靠“自身作用”,從一個冷源轉移到一個熱源中去。這就是說,能量只有從高溫轉移到低溫量,才可以用來作功。因此,例如在一個熱發電機中,熱量與機械功的轉換只有在其中一部分熱量保留下來,不轉變成功的前提下才能產生。
2.氣體定律
波義耳定律:如果溫度不變,壓力與容積的乘積也不變。其關系為:
P1×V1=P2×V2
式中:
P=絕對壓力(Pa),V=容積(m3)
即如壓縮過程容積減半,則壓力升高1倍。
查理士定律:氣體的容積變化正比于溫度變化。(指壓力不變時℃)。關系式如下:
V1/T1=V2/T2 => △V=(V1/T1)×△T
式中:
V=容積(m3),T=容積溫度(K),
△V=容積差,△T=溫度差
氣體狀態普遍定律是波義耳定律與查理士定律的組合。該狀態表示壓力,容積與溫度之間的關系。當一個參數發生變化,至少會導致到其它兩個參數中的一個參數的變化。關系式如下:
(P×V)/T=R=氣體常數
式中:
P=絕對壓力Pa,V=比容(m3/kg),
T=絕對溫度(K)
R=R/M=氣體常數(J/kg×K)
常數R稱為氣體常數,它只與氣體的性質有關。如單位容積的氣體質量為m,則關系式可寫為:
P×V=m×R×T
式中:
P=絕對壓力(Pa),V=容積(m3),
m=莫爾質量(kmo1)-
R=通用氣體常數=8314(J/KMO1×K),
T=絕對溫度(K)
3.傳熱
物體內或不同物體之間的熱量差,終究會導致熱的傳遞,從而達到溫度平衡。這種熱傳遞有三種方式:傳導、對流與輻射實際上熱傳遞是以三種方式同時進行的。
傳導發生在兩固體之間和液體或氣體兩薄層之間,運動著的分子將其能量釋放到鄰近的分子。
所有溫度大于K的物體都會產生熱輻射,當熱輻射到達一個物體時,部分的能量被吸收,并轉變為熱。沒有被吸收的輻射,或穿透過物體,或被反射,只有絕對黑體在理論上會完全吸收所有的輻射能。
實際上傳熱是由熱傳導,對流和輻射三種方式傳熱的總和,一般可用下式表示:
q=k×A×△T×t
式中:
q=熱量(J),
k=總傳熱系數(W/m3×K)
A=面積(m2),△T=溫差,T=時間(S)
傳熱經常發生在被一個隔板分開的物體之間。總的傳熱系數取決于隔板的導熱系數及相關兩側的傳熱系數。對于光潔平板,可用下述關系式:
1/k=1/α1+d/λ+1/α2
式中:
α=隔板相關兩側的傳熱系數(W/m2×K),
d=隔板的厚度(m)
λ=隔板的導熱系數(W/m×K),
k=總傳熱系數(W/m2×K)
在一個交換器中,被傳遞的熱量是各點上主熱量差與總傳熱系數的函數。傳熱面積可用下式表示:
Q=k×A×υm
式中:
Q=傳熱量(W),
K=總傳熱系數(Wm2×K)
A=傳熱面積,
υm=對數平均溫差(K)
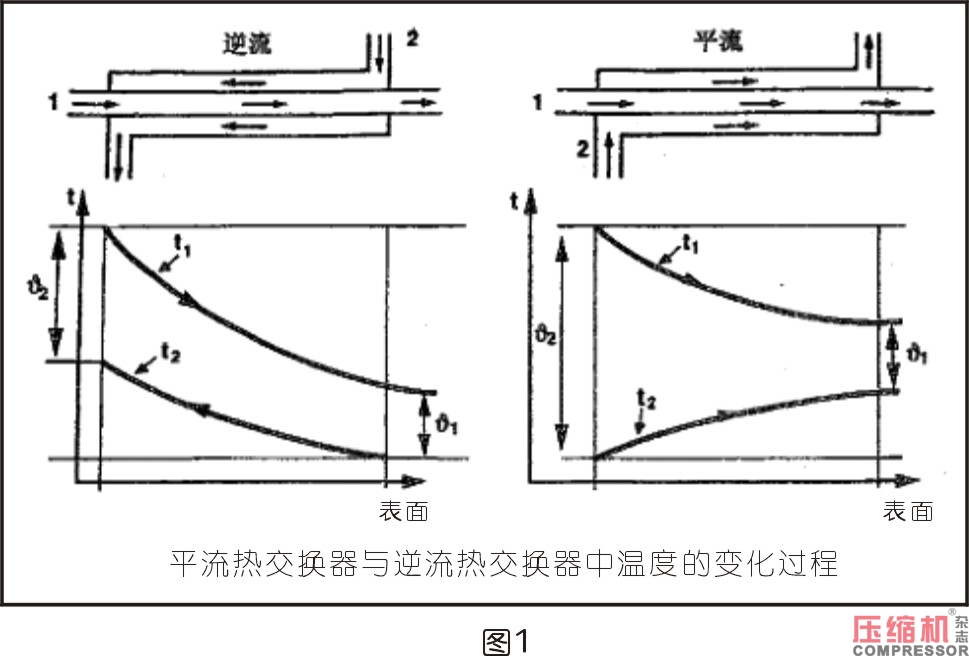
對數平均溫差定義為冷卻器兩連接測溫差的關系,用下式表示:
υm=υ1-υ2/1n(υ1/υ2)
式中:
υm=對數平均溫差(K),
υ=根據圖1所示的溫差
 4.狀態變化
在p/V圖上可以得出氣體從一點到另一點的狀態變化,對于變量p、V和T,實際上需要三個坐標。就狀態變化而言,要沿空間曲面上一條曲線移動,然后就形成狀態的變化。通常人們重視的是曲線在三個平面中的一個平面上的投影,一般是在p/V平面。最基本特征由五個狀態變化構成:等容過程(容積不變),等壓過程(壓力不變),等溫過程(溫度不變),絕熱過程(與周圍沒有熱交換)與多變過程(與周圍的熱交換是以簡單的數學函數表示)。
4.狀態變化
在p/V圖上可以得出氣體從一點到另一點的狀態變化,對于變量p、V和T,實際上需要三個坐標。就狀態變化而言,要沿空間曲面上一條曲線移動,然后就形成狀態的變化。通常人們重視的是曲線在三個平面中的一個平面上的投影,一般是在p/V平面。最基本特征由五個狀態變化構成:等容過程(容積不變),等壓過程(壓力不變),等溫過程(溫度不變),絕熱過程(與周圍沒有熱交換)與多變過程(與周圍的熱交換是以簡單的數學函數表示)。
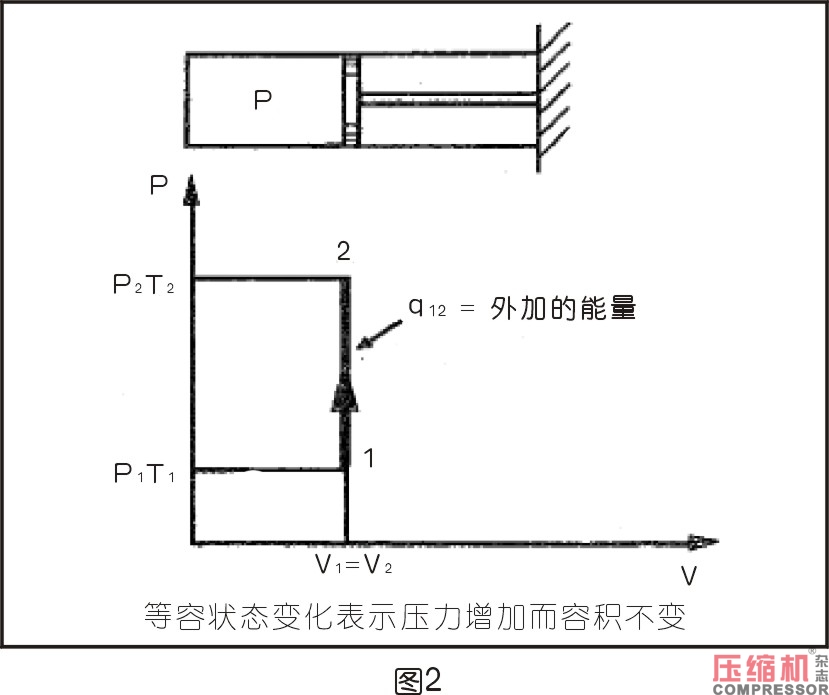 4.1等容過程
加熱一個封閉容器中的氣體,就是等容過程的一個例子,需用熱量的關系式為:
q=m×cv×(T2-T1)
q=熱量(J)
m=質量(kg)
cv=等容比熱(J/kg×K)
T=絕對溫度(K)
4.2等壓過程
4.1等容過程
加熱一個封閉容器中的氣體,就是等容過程的一個例子,需用熱量的關系式為:
q=m×cv×(T2-T1)
q=熱量(J)
m=質量(kg)
cv=等容比熱(J/kg×K)
T=絕對溫度(K)
4.2等壓過程
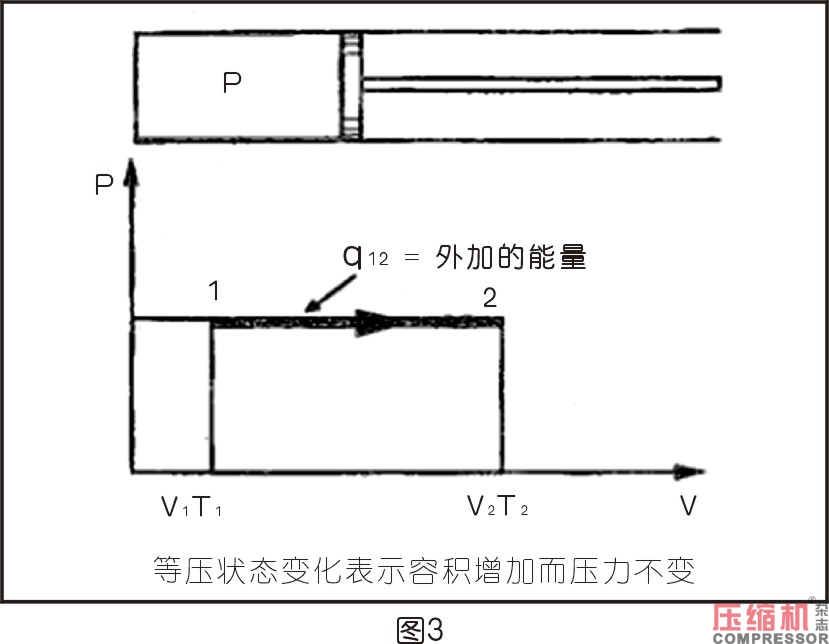 氣缸中的氣體受到恒定載荷活塞的加熱,就是一個等壓過程的例子,所用熱量的關系式如下:
q=m×cp×(T2-T1)
q=熱量(J)
m=質量(kg)
cp=等壓比熱(J/kg×K)
T=絕對溫度(K)
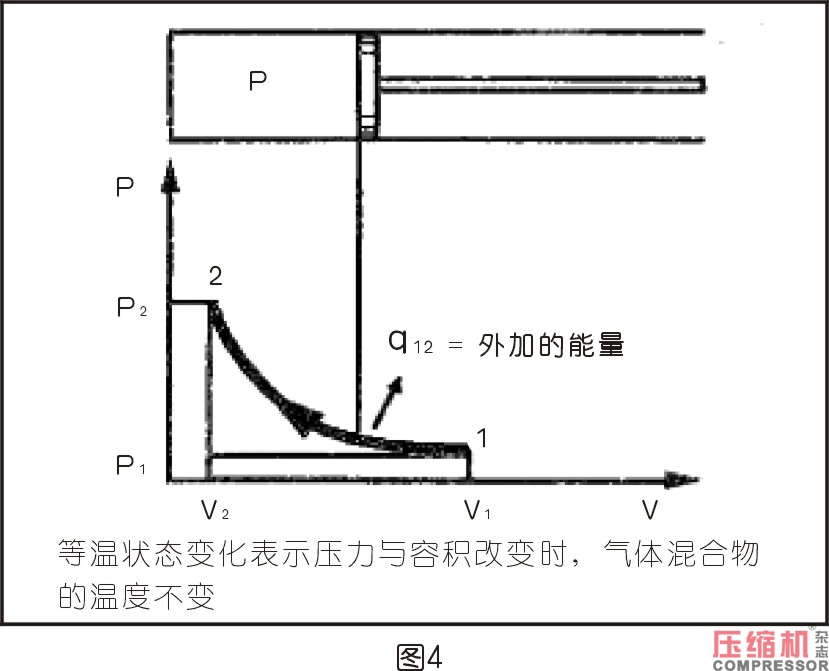
4.3等溫過程
若氣體在氣缸中等溫壓縮,則熱量就等于逐漸進行壓縮所用的功。這實際上是不可能的,因為這么慢的過程無法實現。
產生的熱量關系式如下:
q=m×R×T×1n(p2/p1)及
q=p1×v1×1n(V1/V2)
式中:
q=熱量(J)
m=質量(kg)
R=氣體常數(J/kg×K)
T=絕對溫度(K)
V=容積(m3)
p=絕對壓力(Pa)
氣缸中的氣體受到恒定載荷活塞的加熱,就是一個等壓過程的例子,所用熱量的關系式如下:
q=m×cp×(T2-T1)
q=熱量(J)
m=質量(kg)
cp=等壓比熱(J/kg×K)
T=絕對溫度(K)
4.3等溫過程
若氣體在氣缸中等溫壓縮,則熱量就等于逐漸進行壓縮所用的功。這實際上是不可能的,因為這么慢的過程無法實現。
產生的熱量關系式如下:
q=m×R×T×1n(p2/p1)及
q=p1×v1×1n(V1/V2)
式中:
q=熱量(J)
m=質量(kg)
R=氣體常數(J/kg×K)
T=絕對溫度(K)
V=容積(m3)
p=絕對壓力(Pa)
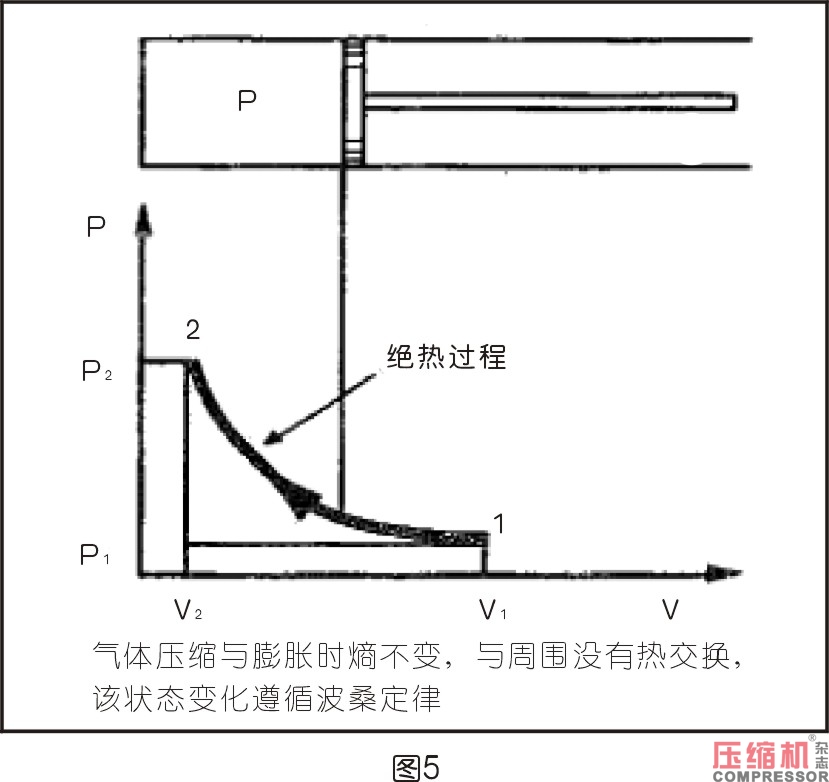
4.4絕熱過程
絕熱過程的一個實例就是氣體在一個完全絕緣與外界沒有熱交換的氣缸中進行壓縮或者氣體通過噴咀快速膨脹,而來不及與周圍進行熱交換。絕熱過程的關系式為:
p2/p1=(V1/V2)k p2/p1=(T2/T1)α
式中:
a=k/(k-1),p=絕對壓力(Pa)
V=容積(m3),T=絕對溫度(K),k=cp/cv
4.5 多變過程
多變過程包括與周圍徹底交換的過程和根本沒有熱交換的絕熱過程。實際上,所有的過程均處在其間,因此將這個通用過程叫做多變過程。
該過程的關系式為:
p×Vn=常數
式中:
p=絕對壓力(pa),v=容積m3,
n=0 表示等壓過程
n=1 表示等溫過程
n=k 表示絕熱過程
n=∞表示等容過程
5.氣流通過噴嘴
通過噴嘴的氣體流量,取決于噴嘴進出口兩側的壓力比,如果噴嘴前的壓力尚未接近于噴嘴后的一倍,流量隨背壓的降低而增加。然而進一步降低噴嘴后的壓力,流量不會再增加。
這就是所謂的臨界壓力比,其大小取決于氣體的絕熱指數(K)。當噴管最小截面上的流速達到音速時,就出現臨界壓力比。
如果噴管后面的壓力進一步下降,低于臨界值,氣流變成為超臨界。通過噴管的流量關系式如下:
G=α×Y×p1×105×A×√(2/(R×T1))
式中:
G=質量流量(kg/s),
α=噴管系數,
Y=流量系數,
A=最小通流量面積(m2)
R=氣體常數(J/kg×K),
T1=噴管前絕對溫度(K),
P1=噴管前絕對壓力(bar)
6.通過管道的流量
雷諾數是一個無因次量,表示流動介質中慣性力與摩擦力之比。定義如下:
Re=D×w×η/ρ=D×w/v
式中:
D=特征量值(m)(例如圓管直徑),
w=平均流速,
ρ=流動介質的密度(kg/m3)
η=流動介質的動力粘度(pv×s)
v=η/ρ=流動介質的運動粘度(m2/s)
原則上說,管內流動有兩種形式。當Re<2000,流體介質內粘性力起主導作用,流動成為層流。就是說介質的不同層次之間彼此良好有次序的運動。層流層斷面速度分布通常呈拋物線形狀。當Re≥4000,慣性力在介質中起主導作用,流動成為紊流形。流動橫截面上流體微團成無規則運動。紊流層斷面的流速分布成為漫散形。
在過渡區,Re≥2000與Re<4000之間,流態是不穩定的。既可以是層流也可以是紊流,或者是兩者的混合。其狀態受管道表面光滑度、外來干擾等諸多因素的影響。
流體能在管內中流動,需要一定的壓差或壓降,以克服管道及連接件的阻力。壓降的大小取決于管徑、管長、管子形狀以及表面光潔度和雷諾數。
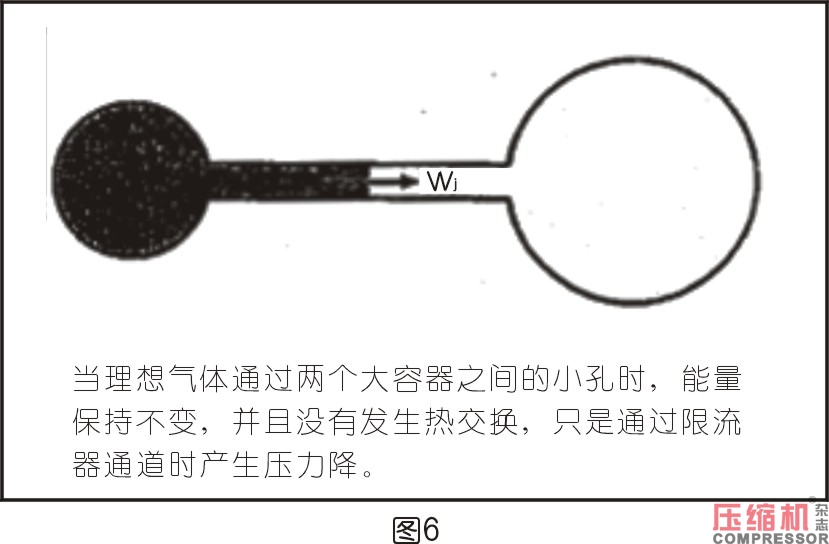
7.節流
理想氣體通過孔板壓力不變,孔板前后溫度也不變。實際上在孔板斷面處產生壓降,內能轉換成動能,這就是溫度下降的原因。對于實際氣體,這種溫度變化成為持久的,即使氣體的能量總量不變。這就是所謂焦耳湯姆遜效應。溫度的變化就等于通過節流截面的壓力變化乘以焦耳湯姆遜系數。
如果流動介質有足夠低的溫度(≤329℃的空氣),通過孔板截面就產生溫降。但如果流動介質的溫度更高,就產生溫升。這種狀況被用于某些技術領域,例如冷凍技術與氣體分離。
來源:本站原創
材料學、機械設計等等。而熱力學就屬于極為重要的一部分,從業者不可不知。本文將對空壓機中涉及到的熱力學相關知識進行分享,希望對大家起到參考作用。
1.基本定律
熱力學第一基礎定律是一個自然界的規律,無法證明,但卻為人們義無反顧地所接受。它既不能被創造也不會被消滅。熱力學第二規律說:熱是永遠無法靠“自身作用”,從一個冷源轉移到一個熱源中去。這就是說,能量只有從高溫轉移到低溫量,才可以用來作功。因此,例如在一個熱發電機中,熱量與機械功的轉換只有在其中一部分熱量保留下來,不轉變成功的前提下才能產生。
2.氣體定律
波義耳定律:如果溫度不變,壓力與容積的乘積也不變。其關系為:
P1×V1=P2×V2
式中:
P=絕對壓力(Pa),V=容積(m3)
即如壓縮過程容積減半,則壓力升高1倍。
查理士定律:氣體的容積變化正比于溫度變化。(指壓力不變時℃)。關系式如下:
V1/T1=V2/T2 => △V=(V1/T1)×△T
式中:
V=容積(m3),T=容積溫度(K),
△V=容積差,△T=溫度差
氣體狀態普遍定律是波義耳定律與查理士定律的組合。該狀態表示壓力,容積與溫度之間的關系。當一個參數發生變化,至少會導致到其它兩個參數中的一個參數的變化。關系式如下:
(P×V)/T=R=氣體常數
式中:
P=絕對壓力Pa,V=比容(m3/kg),
T=絕對溫度(K)
R=R/M=氣體常數(J/kg×K)
常數R稱為氣體常數,它只與氣體的性質有關。如單位容積的氣體質量為m,則關系式可寫為:
P×V=m×R×T
式中:
P=絕對壓力(Pa),V=容積(m3),
m=莫爾質量(kmo1)-
R=通用氣體常數=8314(J/KMO1×K),
T=絕對溫度(K)
3.傳熱
物體內或不同物體之間的熱量差,終究會導致熱的傳遞,從而達到溫度平衡。這種熱傳遞有三種方式:傳導、對流與輻射實際上熱傳遞是以三種方式同時進行的。
傳導發生在兩固體之間和液體或氣體兩薄層之間,運動著的分子將其能量釋放到鄰近的分子。
所有溫度大于K的物體都會產生熱輻射,當熱輻射到達一個物體時,部分的能量被吸收,并轉變為熱。沒有被吸收的輻射,或穿透過物體,或被反射,只有絕對黑體在理論上會完全吸收所有的輻射能。
實際上傳熱是由熱傳導,對流和輻射三種方式傳熱的總和,一般可用下式表示:
q=k×A×△T×t
式中:
q=熱量(J),
k=總傳熱系數(W/m3×K)
A=面積(m2),△T=溫差,T=時間(S)
傳熱經常發生在被一個隔板分開的物體之間。總的傳熱系數取決于隔板的導熱系數及相關兩側的傳熱系數。對于光潔平板,可用下述關系式:
1/k=1/α1+d/λ+1/α2
式中:
α=隔板相關兩側的傳熱系數(W/m2×K),
d=隔板的厚度(m)
λ=隔板的導熱系數(W/m×K),
k=總傳熱系數(W/m2×K)
在一個交換器中,被傳遞的熱量是各點上主熱量差與總傳熱系數的函數。傳熱面積可用下式表示:
Q=k×A×υm
式中:
Q=傳熱量(W),
K=總傳熱系數(Wm2×K)
A=傳熱面積,
υm=對數平均溫差(K)
對數平均溫差定義為冷卻器兩連接測溫差的關系,用下式表示:
υm=υ1-υ2/1n(υ1/υ2)
式中:
υm=對數平均溫差(K),
υ=根據圖1所示的溫差

4.狀態變化
在p/V圖上可以得出氣體從一點到另一點的狀態變化,對于變量p、V和T,實際上需要三個坐標。就狀態變化而言,要沿空間曲面上一條曲線移動,然后就形成狀態的變化。通常人們重視的是曲線在三個平面中的一個平面上的投影,一般是在p/V平面。最基本特征由五個狀態變化構成:等容過程(容積不變),等壓過程(壓力不變),等溫過程(溫度不變),絕熱過程(與周圍沒有熱交換)與多變過程(與周圍的熱交換是以簡單的數學函數表示)。

4.1等容過程
加熱一個封閉容器中的氣體,就是等容過程的一個例子,需用熱量的關系式為:
q=m×cv×(T2-T1)
q=熱量(J)
m=質量(kg)
cv=等容比熱(J/kg×K)
T=絕對溫度(K)
4.2等壓過程

氣缸中的氣體受到恒定載荷活塞的加熱,就是一個等壓過程的例子,所用熱量的關系式如下:
q=m×cp×(T2-T1)
q=熱量(J)
m=質量(kg)
cp=等壓比熱(J/kg×K)
T=絕對溫度(K)
4.3等溫過程
若氣體在氣缸中等溫壓縮,則熱量就等于逐漸進行壓縮所用的功。這實際上是不可能的,因為這么慢的過程無法實現。
產生的熱量關系式如下:
q=m×R×T×1n(p2/p1)及
q=p1×v1×1n(V1/V2)
式中:
q=熱量(J)
m=質量(kg)
R=氣體常數(J/kg×K)
T=絕對溫度(K)
V=容積(m3)
p=絕對壓力(Pa)

4.4絕熱過程
絕熱過程的一個實例就是氣體在一個完全絕緣與外界沒有熱交換的氣缸中進行壓縮或者氣體通過噴咀快速膨脹,而來不及與周圍進行熱交換。絕熱過程的關系式為:
p2/p1=(V1/V2)k p2/p1=(T2/T1)α
式中:
a=k/(k-1),p=絕對壓力(Pa)
V=容積(m3),T=絕對溫度(K),k=cp/cv

4.5 多變過程
多變過程包括與周圍徹底交換的過程和根本沒有熱交換的絕熱過程。實際上,所有的過程均處在其間,因此將這個通用過程叫做多變過程。
該過程的關系式為:
p×Vn=常數
式中:
p=絕對壓力(pa),v=容積m3,
n=0 表示等壓過程
n=1 表示等溫過程
n=k 表示絕熱過程
n=∞表示等容過程
5.氣流通過噴嘴
通過噴嘴的氣體流量,取決于噴嘴進出口兩側的壓力比,如果噴嘴前的壓力尚未接近于噴嘴后的一倍,流量隨背壓的降低而增加。然而進一步降低噴嘴后的壓力,流量不會再增加。
這就是所謂的臨界壓力比,其大小取決于氣體的絕熱指數(K)。當噴管最小截面上的流速達到音速時,就出現臨界壓力比。
如果噴管后面的壓力進一步下降,低于臨界值,氣流變成為超臨界。通過噴管的流量關系式如下:
G=α×Y×p1×105×A×√(2/(R×T1))
式中:
G=質量流量(kg/s),
α=噴管系數,
Y=流量系數,
A=最小通流量面積(m2)
R=氣體常數(J/kg×K),
T1=噴管前絕對溫度(K),
P1=噴管前絕對壓力(bar)
6.通過管道的流量
雷諾數是一個無因次量,表示流動介質中慣性力與摩擦力之比。定義如下:
Re=D×w×η/ρ=D×w/v
式中:
D=特征量值(m)(例如圓管直徑),
w=平均流速,
ρ=流動介質的密度(kg/m3)
η=流動介質的動力粘度(pv×s)
v=η/ρ=流動介質的運動粘度(m2/s)
原則上說,管內流動有兩種形式。當Re<2000,流體介質內粘性力起主導作用,流動成為層流。就是說介質的不同層次之間彼此良好有次序的運動。層流層斷面速度分布通常呈拋物線形狀。當Re≥4000,慣性力在介質中起主導作用,流動成為紊流形。流動橫截面上流體微團成無規則運動。紊流層斷面的流速分布成為漫散形。
在過渡區,Re≥2000與Re<4000之間,流態是不穩定的。既可以是層流也可以是紊流,或者是兩者的混合。其狀態受管道表面光滑度、外來干擾等諸多因素的影響。
流體能在管內中流動,需要一定的壓差或壓降,以克服管道及連接件的阻力。壓降的大小取決于管徑、管長、管子形狀以及表面光潔度和雷諾數。

7.節流
理想氣體通過孔板壓力不變,孔板前后溫度也不變。實際上在孔板斷面處產生壓降,內能轉換成動能,這就是溫度下降的原因。對于實際氣體,這種溫度變化成為持久的,即使氣體的能量總量不變。這就是所謂焦耳湯姆遜效應。溫度的變化就等于通過節流截面的壓力變化乘以焦耳湯姆遜系數。
如果流動介質有足夠低的溫度(≤329℃的空氣),通過孔板截面就產生溫降。但如果流動介質的溫度更高,就產生溫升。這種狀況被用于某些技術領域,例如冷凍技術與氣體分離。
來源:本站原創




網友評論
條評論
最新評論