【壓縮機網】美國石油學會(API)最近實施了離心式壓縮機轉子動力學穩定性的新規范,規范包含了Level I。作為迷宮密封和氣動激勵的不穩定效應的近似,修正的Alford方程用于估計不穩定的影響作用。如果壓縮機不滿足Level I規范,那就采用更復雜的Level II分析,這需要更詳細的迷宮密封分析。
本文考慮了現代高壓離心壓縮機的五個典型不穩定情況的實例。在應用API I級和II級穩定性分析后,進行了設計更改優化以穩定壓縮機。對于這些情況,API穩定性規范用于識別對轉子穩定性影響最大的部件。對平衡活塞密封和葉輪密封進行了具體詳細的分析。將修正的Alford方程應用于多級壓縮機,用于分析其適用性,并與全迷宮密封分析進行了比較。討論了迷宮密封分析的重要因素,如密封間隙效應、入口渦流效應、間隙效應。最后,提出了一種計算迷宮密封交叉耦合力的方法。對于所有五個實例壓縮機,與迷宮計算力相比,修正的Alford力將導致出現最差的穩定性水平。
前言
隨著轉速和額定功率的提高,離心壓縮機的轉子不穩定性成為20世紀60年代的一個主要問題。不穩定的壓縮機具有很高的次同步振動,其振動頻率與轉子的第一基本固有頻率一致。20世紀70年代初,兩個著名和經典的離心壓縮機不穩定情況被稱為Kaybob(史米斯,1975;FoeLee and Males,1975)和Ekofisk(Grouy, 等人,1976)。這兩個問題的解決方案代價高昂,費時費力,最終對轉子進行了重新設計。
基于這些經驗結果,轉子系統穩定性的評估已經成為轉子動力學分析和旋轉機械設計的重要部分。最常見的是,最低或第一模態,對應于轉子的第一基本固有頻率,再次被激發后,將導致次同步振動和轉子不穩定。穩定性或阻尼固有頻率分析的主要結果是對方程解的根值或特征值的處理,一方面通過實部進行穩定性預測,另一方面,通過虛部來預測不穩定頻率。
本文的主要目的是考察幾種工業離心壓縮機的穩定性結果。通過與Kirk(1988a,1988b,1990)的API Level II的迷宮密封計算力的比較,對API Level I修正的Alford交叉耦合力進行了計算,以確定它是否確實可近似為一個保守的壓縮機失穩力。此外,進行了詳細的迷宮密封分析,以確定哪些參數是影響離心壓縮機穩定性的關鍵因素,主要包括軸承間隙公差范圍、迷宮密封間隙和迷宮密封入口渦流效應等參數。
KAYBOB不穩定性
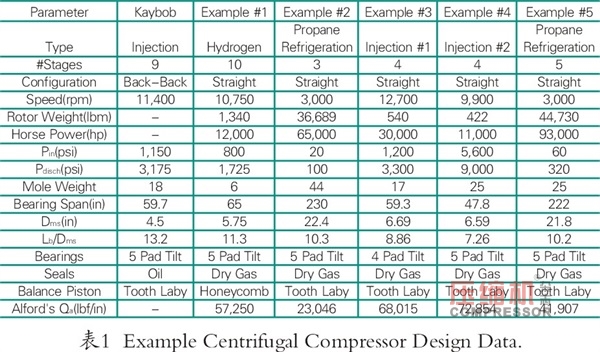
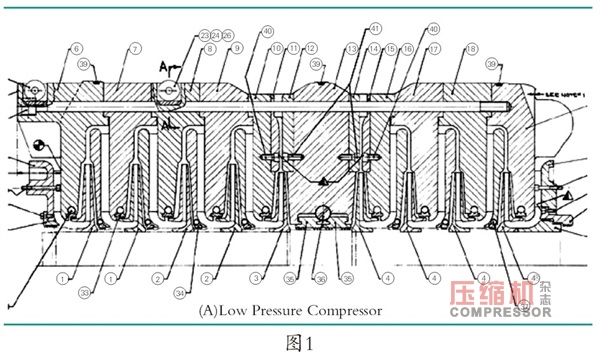
首先將簡要介紹Kaybob不穩定性(Smith,1975;FoeLee and Males,1975)。該九級低壓天然氣噴射壓縮機于1971在加拿大阿爾伯塔投產。關鍵運行參數總結在表1中。最大持續速度(MCS)為11400rpm,入口壓力1150 psi,出口壓力3175 psi,18MW氣體。軸承跨度Lb,與中軸直徑Dms之比為13.2,表明軸非常的有彈性。壓縮機的橫截面如圖1所示。
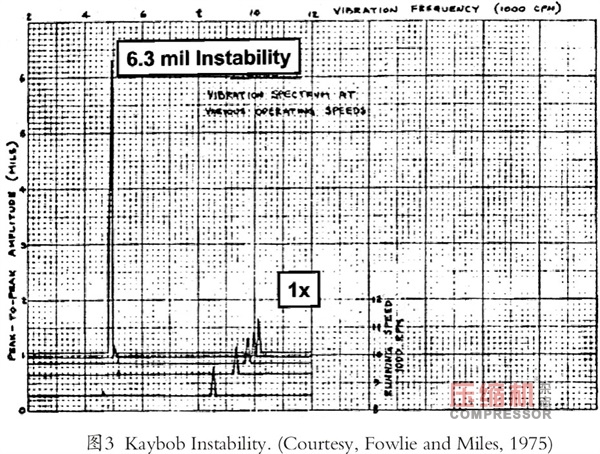
 不穩定性的嚴重程度可以在圖2的軸心軌跡上看到。通過觀察,五瓦塊可傾瓦滑動軸承的輪廓線在6×9mils的峰-峰值軸心軌跡圖中非常明顯。圖3中,突然出現的6.3mils的不穩定現象,顯然是一種次同步振動,是由激發起的壓縮機一階臨界轉速所致。
不穩定性的嚴重程度可以在圖2的軸心軌跡上看到。通過觀察,五瓦塊可傾瓦滑動軸承的輪廓線在6×9mils的峰-峰值軸心軌跡圖中非常明顯。圖3中,突然出現的6.3mils的不穩定現象,顯然是一種次同步振動,是由激發起的壓縮機一階臨界轉速所致。

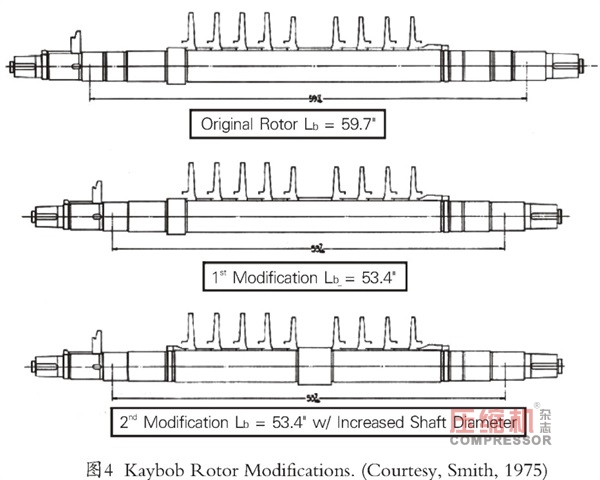
 消除不穩定性的嘗試包括軸承重新設計、油封修改、迷宮密封修改、平衡活塞修改、無葉擴散器改型、擠壓油膜阻尼器改型,以及最后至少兩個轉子重新設計(圖4)。第二轉子重新設計包括增加中軸直徑。最初,使用現有的葉輪鍛件,切割和焊接葉輪輪轂,以增加葉輪內徑以適應軸直徑的增加(圖5)。
消除不穩定性的嘗試包括軸承重新設計、油封修改、迷宮密封修改、平衡活塞修改、無葉擴散器改型、擠壓油膜阻尼器改型,以及最后至少兩個轉子重新設計(圖4)。第二轉子重新設計包括增加中軸直徑。最初,使用現有的葉輪鍛件,切割和焊接葉輪輪轂,以增加葉輪內徑以適應軸直徑的增加(圖5)。
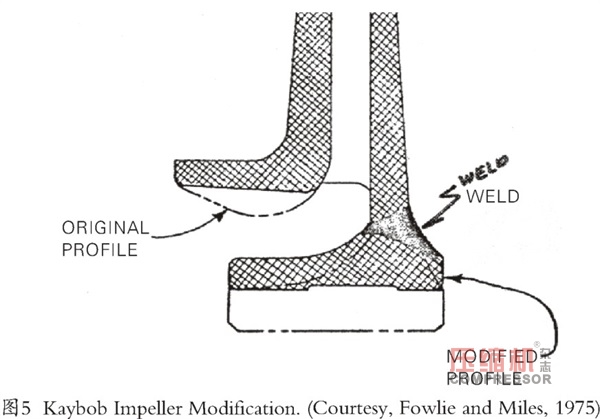 顯然,這種努力代價高昂。然而,它與Ekofisk不穩定性問題一起,提供了改進分析的可能,最終呈現出來現有的穩定性和迷宮密封型式以及新的API穩定性規范。
顯然,這種努力代價高昂。然而,它與Ekofisk不穩定性問題一起,提供了改進分析的可能,最終呈現出來現有的穩定性和迷宮密封型式以及新的API穩定性規范。
對數衰減率
穩定性分析和API穩定性驗收準則的關鍵參數是對數衰減率。對數衰減率是自由振蕩衰減率的量度,也是確定系統中存在的阻尼參數的簡便方法。阻尼值越大,衰減率越快,系統的穩定性也越好。
對數衰減率被定義為任何兩個連續振幅的比值的自然對數。參考圖6,對數衰減率定義為:

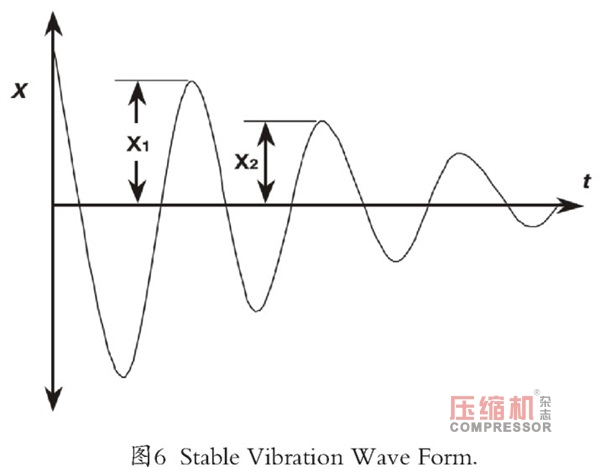 對于穩定的系統,具有正的衰減速率,對數衰減率為正。對于具有負衰減率的不穩定系統,對數衰減率為負。具有正對數衰減率的穩定系統包含足夠的阻尼來克服初始激勵。由此產生的位移將隨著時間消散。相反,對數衰減率為負值的不穩定系統,沒有足夠的阻尼來克服初始激勵,隨著時間的推移將導致位移增加。
對數衰減率也可以用特征值的實部s和虛部ωd表達:
對于穩定的系統,具有正的衰減速率,對數衰減率為正。對于具有負衰減率的不穩定系統,對數衰減率為負。具有正對數衰減率的穩定系統包含足夠的阻尼來克服初始激勵。由此產生的位移將隨著時間消散。相反,對數衰減率為負值的不穩定系統,沒有足夠的阻尼來克服初始激勵,隨著時間的推移將導致位移增加。
對數衰減率也可以用特征值的實部s和虛部ωd表達:
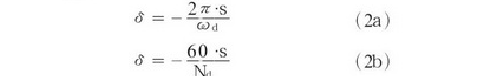 有阻尼固有頻率可以有兩種表達,或采用ωd,單位為rad/s,或采用Nd,單位為rpm。
例1: 12000HP,10級氫離心壓縮機
第一個例子是一個10級12000馬力氫離心壓縮機,具有65英寸的軸承跨度,Lb/Dms為11.3。轉子重1340磅,在10750轉/分的最大持續速度(MCS)下運行,干氣密封和五瓦塊可傾瓦滑動軸承如表1。
有阻尼固有頻率可以有兩種表達,或采用ωd,單位為rad/s,或采用Nd,單位為rpm。
例1: 12000HP,10級氫離心壓縮機
第一個例子是一個10級12000馬力氫離心壓縮機,具有65英寸的軸承跨度,Lb/Dms為11.3。轉子重1340磅,在10750轉/分的最大持續速度(MCS)下運行,干氣密封和五瓦塊可傾瓦滑動軸承如表1。
入口壓力為800 psi,排氣壓力為1725 psi,氣體摩爾質量為6。對數衰減率在零氣動交叉耦合剛度下,在最小軸承間隙下Q為0.26,在最大軸承間隙下為0.40。從API規范617,第七版(2002),修正的Alford方程是:
 βc=3.0
hp=12,000 hp (total all stages)
Hc=Varies stage-to-stage
Dc=Varies stage-to-stage
N =10,750 rpm
ρratio=1.5 (total across compressor)
每級的Q均可由上述公式計算。由于每級的密度比和馬力并不完全一致,因此每級馬力被假定為上述總值的十分之一。每級密度比按上述總密度比假定,達到1/10的功率。葉輪出口寬度和葉輪直徑是級間變量。所有10個Q值的總和是API Alford計算出來的,預期的交叉耦合值Qa為57250lbf/in。QA集中在轉子中跨,得到的對數衰減率為:最小軸承間隙下為-0.4,最大軸承間隙下為-0.23。而API穩定性判定準則是對數衰減率大于0.1。因此,需要進行II級分析。
在進行分析之前,已經決定在平衡活塞上使用蜂窩密封。因此,上文中的穩定性結果包括蜂窩密封動態特性(Scharrer and Pelletti, 1994)。
以迷宮密封幾何形狀、級氣體特性和級壓力作為輸入,對10個葉輪密封件中的每一個進行迷宮密封分析(Kirk,1990)。在密封入口處的氣體渦流值被假定為0.6(對應于轉速的60%)。保守起見,考慮密封件和密封套的加工公差范圍,使用最小的密封間隙。10個迷宮密封總的Q為15700lbf/in。
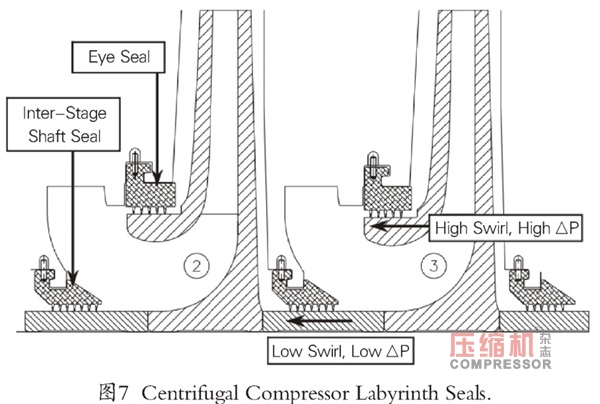
忽略軸上密封作用,因為此處壓降值很低。另外,密封流從靜止部分進入密封,因此,入口渦流值低于密封渦流(圖7)。高入口渦流將導致高Q值。
βc=3.0
hp=12,000 hp (total all stages)
Hc=Varies stage-to-stage
Dc=Varies stage-to-stage
N =10,750 rpm
ρratio=1.5 (total across compressor)
每級的Q均可由上述公式計算。由于每級的密度比和馬力并不完全一致,因此每級馬力被假定為上述總值的十分之一。每級密度比按上述總密度比假定,達到1/10的功率。葉輪出口寬度和葉輪直徑是級間變量。所有10個Q值的總和是API Alford計算出來的,預期的交叉耦合值Qa為57250lbf/in。QA集中在轉子中跨,得到的對數衰減率為:最小軸承間隙下為-0.4,最大軸承間隙下為-0.23。而API穩定性判定準則是對數衰減率大于0.1。因此,需要進行II級分析。
在進行分析之前,已經決定在平衡活塞上使用蜂窩密封。因此,上文中的穩定性結果包括蜂窩密封動態特性(Scharrer and Pelletti, 1994)。
以迷宮密封幾何形狀、級氣體特性和級壓力作為輸入,對10個葉輪密封件中的每一個進行迷宮密封分析(Kirk,1990)。在密封入口處的氣體渦流值被假定為0.6(對應于轉速的60%)。保守起見,考慮密封件和密封套的加工公差范圍,使用最小的密封間隙。10個迷宮密封總的Q為15700lbf/in。
忽略軸上密封作用,因為此處壓降值很低。另外,密封流從靜止部分進入密封,因此,入口渦流值低于密封渦流(圖7)。高入口渦流將導致高Q值。
 由于總的密封Q集中在轉子中心,因此得到的對數衰減率,對應于最小軸承間隙為0.08,對應于最大軸承間隙為0.28。
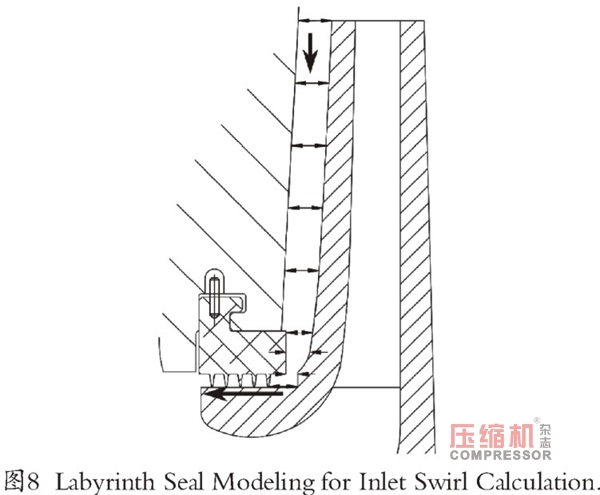
除了估計迷宮密封處的入口渦流,還可以通過模擬葉輪表面和靜止件之間的間隙來計算,如圖8(Kirk,1990)。隨著葉輪間隙模型的引入,入口渦流計算值為0.52,得到的Q值為7600 Lbf/in時的所有密封。由于總的密封Q集中在轉子中心,所得對數衰減率值分別為:最小軸承間隙為0.17,最大軸承間隙為0.35。與I級分析一樣,II級的API穩定性驗收準則是大于0.1的對數衰減率。因此,該壓縮機在軸承間隙公差范圍內滿足API要求。
由于總的密封Q集中在轉子中心,因此得到的對數衰減率,對應于最小軸承間隙為0.08,對應于最大軸承間隙為0.28。
除了估計迷宮密封處的入口渦流,還可以通過模擬葉輪表面和靜止件之間的間隙來計算,如圖8(Kirk,1990)。隨著葉輪間隙模型的引入,入口渦流計算值為0.52,得到的Q值為7600 Lbf/in時的所有密封。由于總的密封Q集中在轉子中心,所得對數衰減率值分別為:最小軸承間隙為0.17,最大軸承間隙為0.35。與I級分析一樣,II級的API穩定性驗收準則是大于0.1的對數衰減率。因此,該壓縮機在軸承間隙公差范圍內滿足API要求。
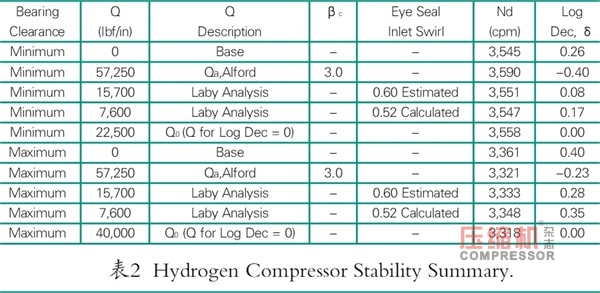
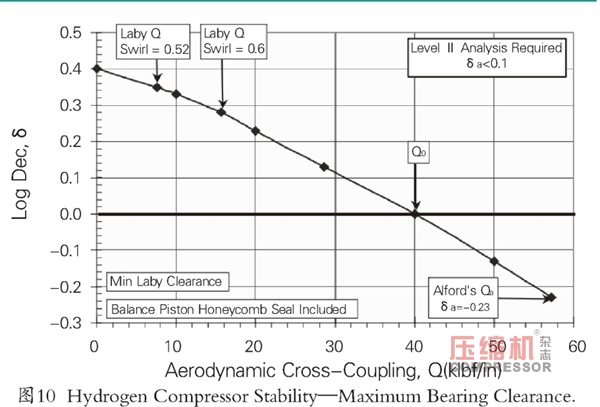
 結果如表2所示,分別在圖9和圖10中給出了最小和最大軸承間隙。從圖9和圖10中也可以注意到零對數衰減率時的Q值,Q0。這些分別為22500和40000lbf/in的最小和最大軸承間隙。顯然,使用改進的Alford力預測的穩定性水平較為保守。
結果如表2所示,分別在圖9和圖10中給出了最小和最大軸承間隙。從圖9和圖10中也可以注意到零對數衰減率時的Q值,Q0。這些分別為22500和40000lbf/in的最小和最大軸承間隙。顯然,使用改進的Alford力預測的穩定性水平較為保守。

 密封入口渦流效應
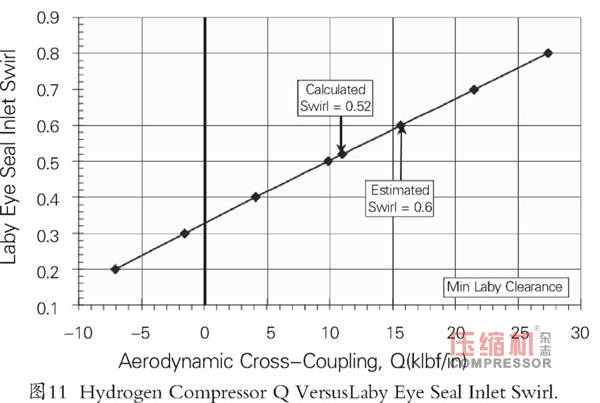
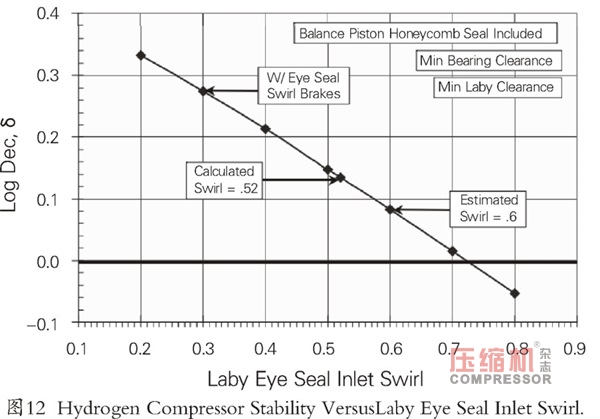
入口渦流對總密封Q的影響如圖11所示。在圖12中給出了相應的穩定性影響。需要注意的是,在最小軸承和密封間隙下,入口渦流值為0.3時,對數衰減率將提高到提高0.28。(Childs and Ramsey, 1991;Moore and Hill, 2000)
密封入口渦流效應
入口渦流對總密封Q的影響如圖11所示。在圖12中給出了相應的穩定性影響。需要注意的是,在最小軸承和密封間隙下,入口渦流值為0.3時,對數衰減率將提高到提高0.28。(Childs and Ramsey, 1991;Moore and Hill, 2000)
 密封間隙效應
密封間隙對Q的影響如圖13所示。加工直徑公差范圍為16~20mils。假設由于葉輪的離心膨脹,最小直徑密封間隙減小4mils,圖13也給出了直徑為12mils的最小工作間隙。圖14中給出了入口渦流為0.6和最小軸承間隙時對穩定性的影響作用。
密封間隙效應
密封間隙對Q的影響如圖13所示。加工直徑公差范圍為16~20mils。假設由于葉輪的離心膨脹,最小直徑密封間隙減小4mils,圖13也給出了直徑為12mils的最小工作間隙。圖14中給出了入口渦流為0.6和最小軸承間隙時對穩定性的影響作用。

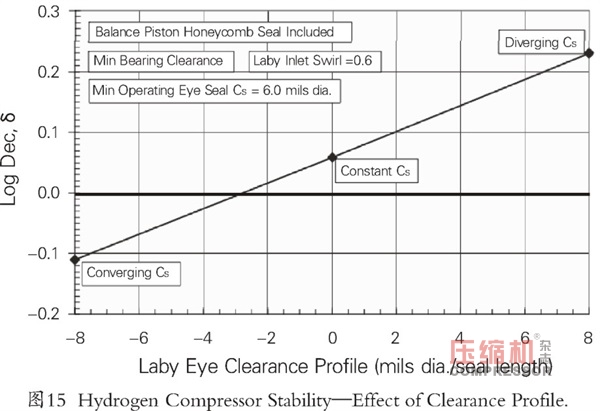
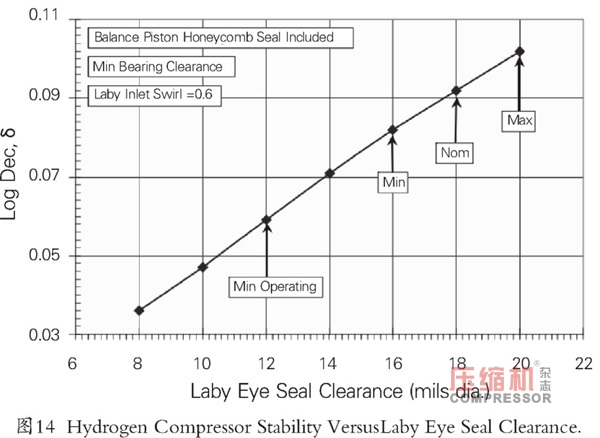 圖15說明了收斂和發散型密封間隙對穩定性的影響。假設所有密封齒均為12mils的直徑間隙,得到的對數衰減率為0.6。如果間隙從密封入口(直徑為16mils)收斂到出口(直徑為8mils),那么對數衰減率將減小到-0.11。反之,從入口(直徑為8mils)到出口(直徑為16mils),那么對數衰減率為0.23。這些計算值的前提條件是:假定最小軸承間隙,并且入口渦流值為0.6。
圖15說明了收斂和發散型密封間隙對穩定性的影響。假設所有密封齒均為12mils的直徑間隙,得到的對數衰減率為0.6。如果間隙從密封入口(直徑為16mils)收斂到出口(直徑為8mils),那么對數衰減率將減小到-0.11。反之,從入口(直徑為8mils)到出口(直徑為16mils),那么對數衰減率為0.23。這些計算值的前提條件是:假定最小軸承間隙,并且入口渦流值為0.6。
 顯然,應該優選發散型的間隙分布,以提高穩定性。對發散型間隙而言,雖然密封主剛度為負,這種影響是最小的。此外,對于發散型間隙情況,泄漏量實際上比恒定間隙減小了。對于這種壓縮機,從密封出口位置增加到密封入口位置,葉輪隨轉速的增大而變化,從而產生不同的密封間隙。
對于發散間隙,這種影響是最小的。此外,泄漏量實際上比恒定間隙減小了發散間隙情況。對于這種壓縮機,葉輪的增長速度從眼睛密封排放位置(葉輪眼)增加到眼睛密封入口位置,從而產生不同的密封間隙。
平衡活塞蜂窩密封
堵塞與入口渦流效應
蜂窩密封的一個問題是蜂窩孔可能堵塞或填充多余物。其它非迷宮式密封也可能存在堵塞,例如孔型密封件。
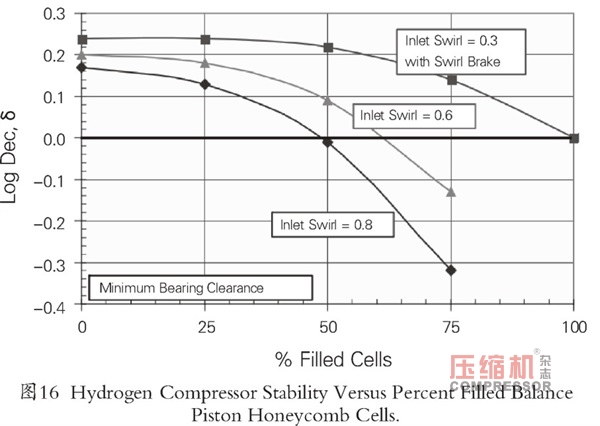
蜂窩密封的這種堵塞孔效應如圖16所示,圖中給出了最小軸承間隙,以及三個不同的蜂窩密封入口渦流值:0.8,一個較糟糕的值;0.6,一個更現實的值;和0.3,模擬包含渦流制動器。結果表明,隨著蜂窩孔的填充或堵塞,穩定性降低。對于入口渦流為0.6的情況,只要有小于48%的孔隙填充,則對數衰減率就會大于0.1,滿足API要求。對于包含渦流制動器(入口渦流為0.3),只要孔隙填充數少于60%,對數衰減率就大于0.1。
顯然,應該優選發散型的間隙分布,以提高穩定性。對發散型間隙而言,雖然密封主剛度為負,這種影響是最小的。此外,對于發散型間隙情況,泄漏量實際上比恒定間隙減小了。對于這種壓縮機,從密封出口位置增加到密封入口位置,葉輪隨轉速的增大而變化,從而產生不同的密封間隙。
對于發散間隙,這種影響是最小的。此外,泄漏量實際上比恒定間隙減小了發散間隙情況。對于這種壓縮機,葉輪的增長速度從眼睛密封排放位置(葉輪眼)增加到眼睛密封入口位置,從而產生不同的密封間隙。
平衡活塞蜂窩密封
堵塞與入口渦流效應
蜂窩密封的一個問題是蜂窩孔可能堵塞或填充多余物。其它非迷宮式密封也可能存在堵塞,例如孔型密封件。
蜂窩密封的這種堵塞孔效應如圖16所示,圖中給出了最小軸承間隙,以及三個不同的蜂窩密封入口渦流值:0.8,一個較糟糕的值;0.6,一個更現實的值;和0.3,模擬包含渦流制動器。結果表明,隨著蜂窩孔的填充或堵塞,穩定性降低。對于入口渦流為0.6的情況,只要有小于48%的孔隙填充,則對數衰減率就會大于0.1,滿足API要求。對于包含渦流制動器(入口渦流為0.3),只要孔隙填充數少于60%,對數衰減率就大于0.1。
 例2:65000 馬力,3級丙烷制冷壓縮機
第二個例子是用于制冷的三級、三段65000 馬力丙烷壓縮機,其具有230inch的軸承跨度和Lb/Dms=10.3。轉子的重量超過36000磅,工作轉速3000rpm,采用干氣密封和五瓦塊可傾瓦滑動軸承(表1)。入口壓力為20 psi,出口壓力為100 psi,氣體摩爾重量為44。大型制冷壓縮機的典型特征是具有較低的對數衰減率和相對較小的不穩定力表現。這臺機器也不例外。該壓縮機的基本對數衰減率(僅就轉子和軸承而言,Q=0)在軸承公差范圍內分布于0.18到0.13不等。
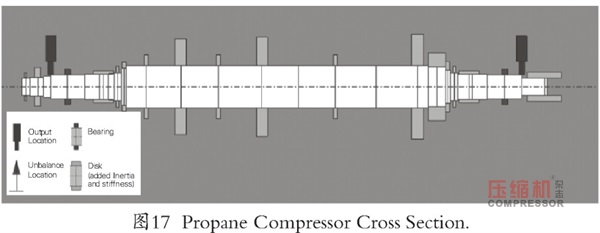
過去對具有多過程段的壓縮機,在考慮“Wachel”型方程(Wachel和Von Nimz,1981)時,出現了適用性問題。在大多數情況下,通過逐級應用修正的Alford方程,已經解決了這些問題。在該應用中,每級表示一個過程段,該過程段內將側流添加到主流中,這發生在第二葉輪和第三葉輪之前。圖17給出了壓縮機的轉子動力學模型。
例2:65000 馬力,3級丙烷制冷壓縮機
第二個例子是用于制冷的三級、三段65000 馬力丙烷壓縮機,其具有230inch的軸承跨度和Lb/Dms=10.3。轉子的重量超過36000磅,工作轉速3000rpm,采用干氣密封和五瓦塊可傾瓦滑動軸承(表1)。入口壓力為20 psi,出口壓力為100 psi,氣體摩爾重量為44。大型制冷壓縮機的典型特征是具有較低的對數衰減率和相對較小的不穩定力表現。這臺機器也不例外。該壓縮機的基本對數衰減率(僅就轉子和軸承而言,Q=0)在軸承公差范圍內分布于0.18到0.13不等。
過去對具有多過程段的壓縮機,在考慮“Wachel”型方程(Wachel和Von Nimz,1981)時,出現了適用性問題。在大多數情況下,通過逐級應用修正的Alford方程,已經解決了這些問題。在該應用中,每級表示一個過程段,該過程段內將側流添加到主流中,這發生在第二葉輪和第三葉輪之前。圖17給出了壓縮機的轉子動力學模型。
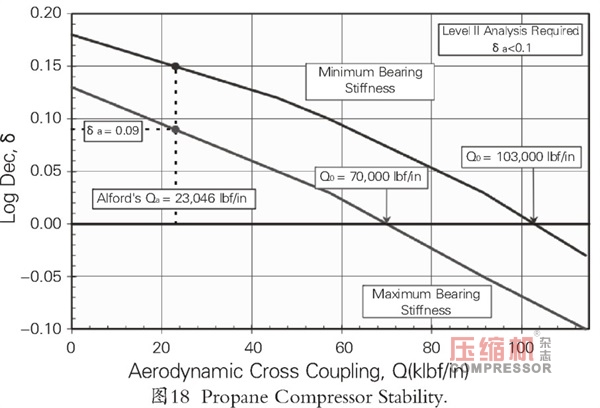 應用公式(3),可以計算預期的不穩定力Qa,總預期的失穩力Qa為23046 lbf/in。將這應用于轉子中心,分別得到最小和最大軸承剛度的對數衰減率為0.15和0.09。圖18顯示了穩定性靈敏度曲線。(軸承間隙和油入口溫度的公差范圍限定了軸承剛度的范圍)。根據API的要求,由于最壞情況δa<0.1,用Kirk(1990)開發的方法進行二級分析,以預測葉輪迷宮式密封件的性能。這些不穩定力被施加在密封的實際位置上。對于相同范圍內的軸承剛度,對數衰減率是針對以下條件計算的:
僅轉子和軸承
轉子、軸承和葉輪迷宮密封
轉子、軸承、葉輪迷宮密封和平衡活塞
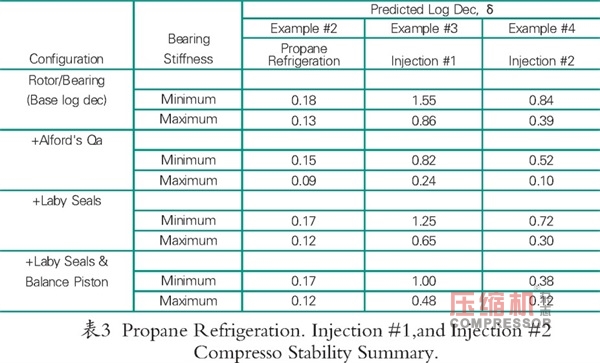
表3包含了二級分析的結果和使用修正的Alford力對轉子穩定性的估計。正如預期的那樣,由于迷宮密封(包括平衡活塞)的激勵力很小,因此對轉子穩定性影響較小。對于這個應用,使用改進的Alford力預測的穩定性水平是保守的。
應用公式(3),可以計算預期的不穩定力Qa,總預期的失穩力Qa為23046 lbf/in。將這應用于轉子中心,分別得到最小和最大軸承剛度的對數衰減率為0.15和0.09。圖18顯示了穩定性靈敏度曲線。(軸承間隙和油入口溫度的公差范圍限定了軸承剛度的范圍)。根據API的要求,由于最壞情況δa<0.1,用Kirk(1990)開發的方法進行二級分析,以預測葉輪迷宮式密封件的性能。這些不穩定力被施加在密封的實際位置上。對于相同范圍內的軸承剛度,對數衰減率是針對以下條件計算的:
僅轉子和軸承
轉子、軸承和葉輪迷宮密封
轉子、軸承、葉輪迷宮密封和平衡活塞
表3包含了二級分析的結果和使用修正的Alford力對轉子穩定性的估計。正如預期的那樣,由于迷宮密封(包括平衡活塞)的激勵力很小,因此對轉子穩定性影響較小。對于這個應用,使用改進的Alford力預測的穩定性水平是保守的。
 例3 30000馬力4級噴射壓縮機(略)
第四個例子是11000馬力的四級離心壓縮機,用于噴射,具有48英寸的軸承跨度,Lb/Dms=7.26。轉子重422磅,運行轉速為9900rpm,采用干氣密封和五瓦塊可傾瓦滑動軸承(表1)。入口壓力為5600 psi,出口壓力為9000 psi。
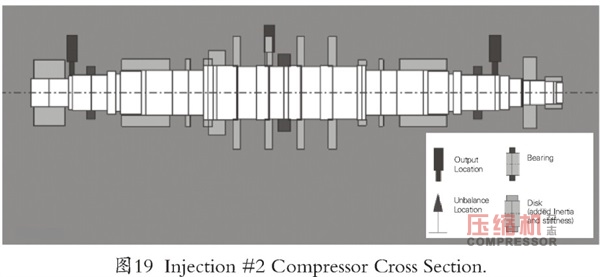
就噴射方面而言,該壓縮機被認為具有較高的排放壓力范圍和中等的功率與重量比值。在這樣的情況下,由于壓縮機中氣體的密度升高,不穩定力預計會更高。實際上,由于平均氣體密度為115 kg/m3,需要進行II級分析。如前所述,制造商保守地設計了具有較大中心軸段的壓縮機,以抵消預期的更高的不穩定力(圖19)。
例3 30000馬力4級噴射壓縮機(略)
第四個例子是11000馬力的四級離心壓縮機,用于噴射,具有48英寸的軸承跨度,Lb/Dms=7.26。轉子重422磅,運行轉速為9900rpm,采用干氣密封和五瓦塊可傾瓦滑動軸承(表1)。入口壓力為5600 psi,出口壓力為9000 psi。
就噴射方面而言,該壓縮機被認為具有較高的排放壓力范圍和中等的功率與重量比值。在這樣的情況下,由于壓縮機中氣體的密度升高,不穩定力預計會更高。實際上,由于平均氣體密度為115 kg/m3,需要進行II級分析。如前所述,制造商保守地設計了具有較大中心軸段的壓縮機,以抵消預期的更高的不穩定力(圖19)。
 這種情況下,修改后的Alford力計算值為72854lbf/in,大致等于示例3中的壓縮機。(圖20)。較高的氣體密度抵消了前面例子中較高的馬力。因此,對于這兩個例子,預期的不穩定力水平大致相同。表3包含了I級和II級分析的穩定性分析結果。與其它噴射壓縮機一樣,由于Q0<2Qa,需要進行II級分析,這表明預期的失穩力和驅動系統不穩定所需的量之間存在足夠的安全余量。
這種情況下,修改后的Alford力計算值為72854lbf/in,大致等于示例3中的壓縮機。(圖20)。較高的氣體密度抵消了前面例子中較高的馬力。因此,對于這兩個例子,預期的不穩定力水平大致相同。表3包含了I級和II級分析的穩定性分析結果。與其它噴射壓縮機一樣,由于Q0<2Qa,需要進行II級分析,這表明預期的失穩力和驅動系統不穩定所需的量之間存在足夠的安全余量。
 如前所述,對于兩個噴射壓縮機來說,Alford不穩定力幾乎相等。表3通過比較兩個II級分析,證實了這一事實。從基礎值到包括所有不穩定力條件,在軸承系數變化范圍內,對于第一噴射壓縮機的對數衰減率大約為-0.55和-0.40,對于第二噴射壓縮機的對數衰減率約為-0.45和-0.30。考慮到轉子和軸承幾何形狀的差異,這兩者可視為相當或一致。與前面的例子不同,平衡活塞產生了大部分的不穩定力。
由于壓縮機內氣體平均密度上升,因此需要進行II級分析。這臺壓縮機成功地通過了滿負荷試驗,沒有發生穩定性問題。
例5 混合制冷
在前三個例子中,通過比較I級和II級分析,得到了對數衰減率值,來確定修正的Alford方程的保守性。在本節中,提出了一種比較等效集中不穩定力的更直接的方法,類似于Memmott (2000)。示例3中,噴射壓縮機與較大的制冷壓縮機一起使用。93000馬力的混合制冷壓縮機(例5)具有222英寸的軸承跨度,Lb/Dms為10.2。圖21比較了這兩種壓縮機。轉子重44730磅,運行轉速為3000rpm,采用干氣密封和五瓦塊可傾瓦滑動軸承(表1)。入口壓力為60 psi,使用25MW的氣體,具有320 psi的出口壓力。
如前所述,對于兩個噴射壓縮機來說,Alford不穩定力幾乎相等。表3通過比較兩個II級分析,證實了這一事實。從基礎值到包括所有不穩定力條件,在軸承系數變化范圍內,對于第一噴射壓縮機的對數衰減率大約為-0.55和-0.40,對于第二噴射壓縮機的對數衰減率約為-0.45和-0.30。考慮到轉子和軸承幾何形狀的差異,這兩者可視為相當或一致。與前面的例子不同,平衡活塞產生了大部分的不穩定力。
由于壓縮機內氣體平均密度上升,因此需要進行II級分析。這臺壓縮機成功地通過了滿負荷試驗,沒有發生穩定性問題。
例5 混合制冷
在前三個例子中,通過比較I級和II級分析,得到了對數衰減率值,來確定修正的Alford方程的保守性。在本節中,提出了一種比較等效集中不穩定力的更直接的方法,類似于Memmott (2000)。示例3中,噴射壓縮機與較大的制冷壓縮機一起使用。93000馬力的混合制冷壓縮機(例5)具有222英寸的軸承跨度,Lb/Dms為10.2。圖21比較了這兩種壓縮機。轉子重44730磅,運行轉速為3000rpm,采用干氣密封和五瓦塊可傾瓦滑動軸承(表1)。入口壓力為60 psi,使用25MW的氣體,具有320 psi的出口壓力。
 為了產生與修正的Alford方程計算等效的失穩力,使用以下關系計算每個密封件的等效交叉耦合剛度:
為了產生與修正的Alford方程計算等效的失穩力,使用以下關系計算每個密封件的等效交叉耦合剛度:
 K和C值由迷宮密封分析(Kirk, 1990)確定,轉子中心的等效模態交叉耦合定義為:
K和C值由迷宮密封分析(Kirk, 1990)確定,轉子中心的等效模態交叉耦合定義為:
 從第一阻尼固有頻率的歸一化模態振型確定模態影響因子Mf,表征密封位置處的位移。對所有密封位置進行求和,得到交叉耦合力。這種模態交叉耦合,Qm,連同II級分析中計算的對數衰減率值一起,在最大軸承剛度的條件下,繪制在兩個壓縮機實例的穩定性靈敏度圖上。
圖22為例子3種第一種噴射壓縮機的結果。
從第一阻尼固有頻率的歸一化模態振型確定模態影響因子Mf,表征密封位置處的位移。對所有密封位置進行求和,得到交叉耦合力。這種模態交叉耦合,Qm,連同II級分析中計算的對數衰減率值一起,在最大軸承剛度的條件下,繪制在兩個壓縮機實例的穩定性靈敏度圖上。
圖22為例子3種第一種噴射壓縮機的結果。
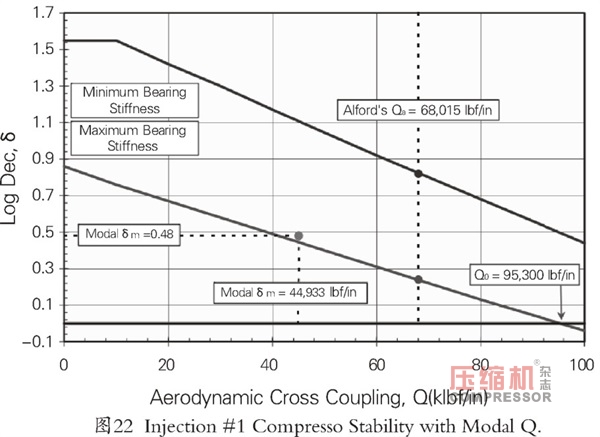
 該壓縮機的最小模態系數僅為0.91,反映了壓縮機的軸具有較好的剛性工作條件(stiffer shaft operation)。考慮到迷宮密封和平衡活塞力,計算模態交叉耦合系數為44933lbf/in。表3中,包括所有不穩定力的II級對數衰減率,在最大支承剛度時,為0.48。在靈敏度圖上繪制這一點,人們發現該點幾乎直接位于通過在轉子中心放置不同量值的交叉耦合剛度而得到的直線上。需要強調的是,對數衰減率繪制的δm是由II級分析計算得到的,考慮位于實際位置的密封效應。從這一點可以得出如下結論:
modal reduction產生的交叉耦合力直接與修正Alford力相媲美。
模態交叉耦合還提供了基于實際密封系數的轉子裕度指示。(在這種情況下,將44933 lbf/in與95300lbf/in的Q0量進行比較。大約存在兩倍安全余量,或更簡單地說,迷宮密封的不穩定效應可能比預測不穩定條件之前的計算值大兩倍。
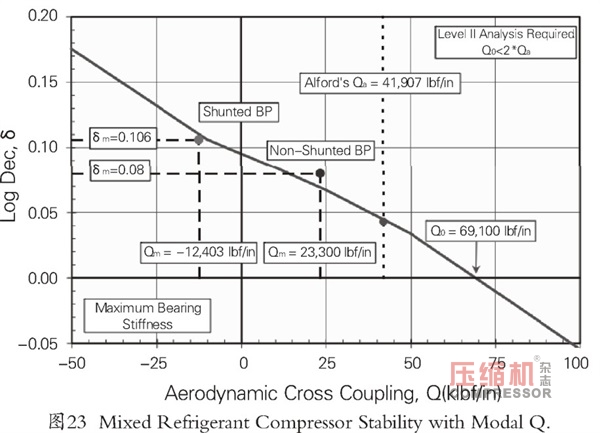
對混合制冷壓縮機進行重復計算(例5)。對于這種壓縮機,最小模態系數為0.56,表示軸具有更靈活的彎曲模態。在II級分析中包括兩種密封結構,一種具有分流的平衡活塞另一種是沒有分流的密封。模態交叉耦合和最終II級對數衰減率值繪制如圖23所示。與噴射壓縮機一樣,這兩個點與I級分析的靈敏度線密切相關。這是真實的情況,即使在分流平衡活塞的情況下,凈交叉耦合項為負(或穩定)。
結論
開展了API水平I級修正的Alford交叉耦合力的計算,并證實了壓縮機的不穩定力是一種保守估計。研究了幾個工業領域的應用,包括氫壓縮機、兩個高壓噴射壓縮機、一個具有高功率與重量比的壓縮機,以及兩個大型制冷壓縮機,包括多級結構。在所有情況下,修正的Alford力,將產生最差的穩定性水平。
此外,檢查了II級分析的細節,以確定哪些參數是確定離心壓縮機穩定性的關鍵。一些已知的影響,包括軸承間隙公差和迷宮密封入口渦流,顯示出對10級氫氣壓縮機的穩定性水平有重大影響。在恒定的入口渦流為0.6的情況下,僅僅將在葉輪密封處的齒隙傾斜從8 mils 徑向收斂區變為8 mils徑向發散區,預測的對數衰減率將從-0.11變為0.23。這為提高離心式離心壓縮機的穩定性提供了另一個簡單的途徑。
最后,提出了一種模態方法來直接比較I級和II級不穩定力。除了確認修正的Alford力的保守性外,模態方法還允許使用穩定性靈敏度曲線來逼近迷宮密封系數相對于零對數衰減率閾值的安全裕度。
參數如下:
Cs=Seal diametral clearance (mils)
C=Principle damping (lbf-sec/in)
Dc=Impeller diameter (inch)
Dms=Midshaft diameter (inch)
Hc=Minimum width of the impeller or discharge volute (inch)
hp=Horsepower (hp)
k=Cross-coupled stiffness (lbf/in)
Lb=Bearing span, (inch)
Mf=Modal influence factor
N=Speed (rpm)
Nd=Damped natural frequency (cpm)
Pdisch=Discharge pressure (psi)
Pin=Inlet pressure (psi)
Q=Aerodynamic cross-coupling (lbf/in)
Qa=Anticipated aerodynamic cross-coupling (lbf/in)
Qeq=Equivalent cross-coupling (lbf/in)
Qm=Modal cross-coupling (lbf/in)
Q0=Aerodynamic cross-coupling for zero log dec (lbf/in)
s=Real part of eigenvalue
X1,2=Amplitude (mils)
β=Efficiency factor δ = Log dec
δa=Log dec for Qa
δm=Final log dec from the Level II analysis
ρratio=Density ratio
ωd=Damped natural frequency (rad/sec)
ωcs=Damped first natural frequency (rad/sec)
該壓縮機的最小模態系數僅為0.91,反映了壓縮機的軸具有較好的剛性工作條件(stiffer shaft operation)。考慮到迷宮密封和平衡活塞力,計算模態交叉耦合系數為44933lbf/in。表3中,包括所有不穩定力的II級對數衰減率,在最大支承剛度時,為0.48。在靈敏度圖上繪制這一點,人們發現該點幾乎直接位于通過在轉子中心放置不同量值的交叉耦合剛度而得到的直線上。需要強調的是,對數衰減率繪制的δm是由II級分析計算得到的,考慮位于實際位置的密封效應。從這一點可以得出如下結論:
modal reduction產生的交叉耦合力直接與修正Alford力相媲美。
模態交叉耦合還提供了基于實際密封系數的轉子裕度指示。(在這種情況下,將44933 lbf/in與95300lbf/in的Q0量進行比較。大約存在兩倍安全余量,或更簡單地說,迷宮密封的不穩定效應可能比預測不穩定條件之前的計算值大兩倍。
對混合制冷壓縮機進行重復計算(例5)。對于這種壓縮機,最小模態系數為0.56,表示軸具有更靈活的彎曲模態。在II級分析中包括兩種密封結構,一種具有分流的平衡活塞另一種是沒有分流的密封。模態交叉耦合和最終II級對數衰減率值繪制如圖23所示。與噴射壓縮機一樣,這兩個點與I級分析的靈敏度線密切相關。這是真實的情況,即使在分流平衡活塞的情況下,凈交叉耦合項為負(或穩定)。
結論
開展了API水平I級修正的Alford交叉耦合力的計算,并證實了壓縮機的不穩定力是一種保守估計。研究了幾個工業領域的應用,包括氫壓縮機、兩個高壓噴射壓縮機、一個具有高功率與重量比的壓縮機,以及兩個大型制冷壓縮機,包括多級結構。在所有情況下,修正的Alford力,將產生最差的穩定性水平。
此外,檢查了II級分析的細節,以確定哪些參數是確定離心壓縮機穩定性的關鍵。一些已知的影響,包括軸承間隙公差和迷宮密封入口渦流,顯示出對10級氫氣壓縮機的穩定性水平有重大影響。在恒定的入口渦流為0.6的情況下,僅僅將在葉輪密封處的齒隙傾斜從8 mils 徑向收斂區變為8 mils徑向發散區,預測的對數衰減率將從-0.11變為0.23。這為提高離心式離心壓縮機的穩定性提供了另一個簡單的途徑。
最后,提出了一種模態方法來直接比較I級和II級不穩定力。除了確認修正的Alford力的保守性外,模態方法還允許使用穩定性靈敏度曲線來逼近迷宮密封系數相對于零對數衰減率閾值的安全裕度。
參數如下:
Cs=Seal diametral clearance (mils)
C=Principle damping (lbf-sec/in)
Dc=Impeller diameter (inch)
Dms=Midshaft diameter (inch)
Hc=Minimum width of the impeller or discharge volute (inch)
hp=Horsepower (hp)
k=Cross-coupled stiffness (lbf/in)
Lb=Bearing span, (inch)
Mf=Modal influence factor
N=Speed (rpm)
Nd=Damped natural frequency (cpm)
Pdisch=Discharge pressure (psi)
Pin=Inlet pressure (psi)
Q=Aerodynamic cross-coupling (lbf/in)
Qa=Anticipated aerodynamic cross-coupling (lbf/in)
Qeq=Equivalent cross-coupling (lbf/in)
Qm=Modal cross-coupling (lbf/in)
Q0=Aerodynamic cross-coupling for zero log dec (lbf/in)
s=Real part of eigenvalue
X1,2=Amplitude (mils)
β=Efficiency factor δ = Log dec
δa=Log dec for Qa
δm=Final log dec from the Level II analysis
ρratio=Density ratio
ωd=Damped natural frequency (rad/sec)
ωcs=Damped first natural frequency (rad/sec)
【壓縮機網】美國石油學會(API)最近實施了離心式壓縮機轉子動力學穩定性的新規范,規范包含了Level I。作為迷宮密封和氣動激勵的不穩定效應的近似,修正的Alford方程用于估計不穩定的影響作用。如果壓縮機不滿足Level I規范,那就采用更復雜的Level II分析,這需要更詳細的迷宮密封分析。
本文考慮了現代高壓離心壓縮機的五個典型不穩定情況的實例。在應用API I級和II級穩定性分析后,進行了設計更改優化以穩定壓縮機。對于這些情況,API穩定性規范用于識別對轉子穩定性影響最大的部件。對平衡活塞密封和葉輪密封進行了具體詳細的分析。將修正的Alford方程應用于多級壓縮機,用于分析其適用性,并與全迷宮密封分析進行了比較。討論了迷宮密封分析的重要因素,如密封間隙效應、入口渦流效應、間隙效應。最后,提出了一種計算迷宮密封交叉耦合力的方法。對于所有五個實例壓縮機,與迷宮計算力相比,修正的Alford力將導致出現最差的穩定性水平。
前言
隨著轉速和額定功率的提高,離心壓縮機的轉子不穩定性成為20世紀60年代的一個主要問題。不穩定的壓縮機具有很高的次同步振動,其振動頻率與轉子的第一基本固有頻率一致。20世紀70年代初,兩個著名和經典的離心壓縮機不穩定情況被稱為Kaybob(史米斯,1975;FoeLee and Males,1975)和Ekofisk(Grouy, 等人,1976)。這兩個問題的解決方案代價高昂,費時費力,最終對轉子進行了重新設計。
基于這些經驗結果,轉子系統穩定性的評估已經成為轉子動力學分析和旋轉機械設計的重要部分。最常見的是,最低或第一模態,對應于轉子的第一基本固有頻率,再次被激發后,將導致次同步振動和轉子不穩定。穩定性或阻尼固有頻率分析的主要結果是對方程解的根值或特征值的處理,一方面通過實部進行穩定性預測,另一方面,通過虛部來預測不穩定頻率。
本文的主要目的是考察幾種工業離心壓縮機的穩定性結果。通過與Kirk(1988a,1988b,1990)的API Level II的迷宮密封計算力的比較,對API Level I修正的Alford交叉耦合力進行了計算,以確定它是否確實可近似為一個保守的壓縮機失穩力。此外,進行了詳細的迷宮密封分析,以確定哪些參數是影響離心壓縮機穩定性的關鍵因素,主要包括軸承間隙公差范圍、迷宮密封間隙和迷宮密封入口渦流效應等參數。
KAYBOB不穩定性
首先將簡要介紹Kaybob不穩定性(Smith,1975;FoeLee and Males,1975)。該九級低壓天然氣噴射壓縮機于1971在加拿大阿爾伯塔投產。關鍵運行參數總結在表1中。最大持續速度(MCS)為11400rpm,入口壓力1150 psi,出口壓力3175 psi,18MW氣體。軸承跨度Lb,與中軸直徑Dms之比為13.2,表明軸非常的有彈性。壓縮機的橫截面如圖1所示。


不穩定性的嚴重程度可以在圖2的軸心軌跡上看到。通過觀察,五瓦塊可傾瓦滑動軸承的輪廓線在6×9mils的峰-峰值軸心軌跡圖中非常明顯。圖3中,突然出現的6.3mils的不穩定現象,顯然是一種次同步振動,是由激發起的壓縮機一階臨界轉速所致。


消除不穩定性的嘗試包括軸承重新設計、油封修改、迷宮密封修改、平衡活塞修改、無葉擴散器改型、擠壓油膜阻尼器改型,以及最后至少兩個轉子重新設計(圖4)。第二轉子重新設計包括增加中軸直徑。最初,使用現有的葉輪鍛件,切割和焊接葉輪輪轂,以增加葉輪內徑以適應軸直徑的增加(圖5)。


顯然,這種努力代價高昂。然而,它與Ekofisk不穩定性問題一起,提供了改進分析的可能,最終呈現出來現有的穩定性和迷宮密封型式以及新的API穩定性規范。
對數衰減率
穩定性分析和API穩定性驗收準則的關鍵參數是對數衰減率。對數衰減率是自由振蕩衰減率的量度,也是確定系統中存在的阻尼參數的簡便方法。阻尼值越大,衰減率越快,系統的穩定性也越好。
對數衰減率被定義為任何兩個連續振幅的比值的自然對數。參考圖6,對數衰減率定義為:



對于穩定的系統,具有正的衰減速率,對數衰減率為正。對于具有負衰減率的不穩定系統,對數衰減率為負。具有正對數衰減率的穩定系統包含足夠的阻尼來克服初始激勵。由此產生的位移將隨著時間消散。相反,對數衰減率為負值的不穩定系統,沒有足夠的阻尼來克服初始激勵,隨著時間的推移將導致位移增加。
對數衰減率也可以用特征值的實部s和虛部ωd表達:
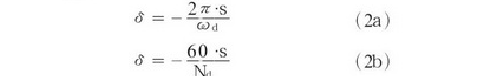
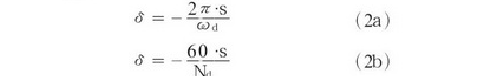
有阻尼固有頻率可以有兩種表達,或采用ωd,單位為rad/s,或采用Nd,單位為rpm。
例1: 12000HP,10級氫離心壓縮機
第一個例子是一個10級12000馬力氫離心壓縮機,具有65英寸的軸承跨度,Lb/Dms為11.3。轉子重1340磅,在10750轉/分的最大持續速度(MCS)下運行,干氣密封和五瓦塊可傾瓦滑動軸承如表1。
入口壓力為800 psi,排氣壓力為1725 psi,氣體摩爾質量為6。對數衰減率在零氣動交叉耦合剛度下,在最小軸承間隙下Q為0.26,在最大軸承間隙下為0.40。從API規范617,第七版(2002),修正的Alford方程是:

βc=3.0
hp=12,000 hp (total all stages)
Hc=Varies stage-to-stage
Dc=Varies stage-to-stage
N =10,750 rpm
ρratio=1.5 (total across compressor)
每級的Q均可由上述公式計算。由于每級的密度比和馬力并不完全一致,因此每級馬力被假定為上述總值的十分之一。每級密度比按上述總密度比假定,達到1/10的功率。葉輪出口寬度和葉輪直徑是級間變量。所有10個Q值的總和是API Alford計算出來的,預期的交叉耦合值Qa為57250lbf/in。QA集中在轉子中跨,得到的對數衰減率為:最小軸承間隙下為-0.4,最大軸承間隙下為-0.23。而API穩定性判定準則是對數衰減率大于0.1。因此,需要進行II級分析。
在進行分析之前,已經決定在平衡活塞上使用蜂窩密封。因此,上文中的穩定性結果包括蜂窩密封動態特性(Scharrer and Pelletti, 1994)。
以迷宮密封幾何形狀、級氣體特性和級壓力作為輸入,對10個葉輪密封件中的每一個進行迷宮密封分析(Kirk,1990)。在密封入口處的氣體渦流值被假定為0.6(對應于轉速的60%)。保守起見,考慮密封件和密封套的加工公差范圍,使用最小的密封間隙。10個迷宮密封總的Q為15700lbf/in。
忽略軸上密封作用,因為此處壓降值很低。另外,密封流從靜止部分進入密封,因此,入口渦流值低于密封渦流(圖7)。高入口渦流將導致高Q值。

由于總的密封Q集中在轉子中心,因此得到的對數衰減率,對應于最小軸承間隙為0.08,對應于最大軸承間隙為0.28。
除了估計迷宮密封處的入口渦流,還可以通過模擬葉輪表面和靜止件之間的間隙來計算,如圖8(Kirk,1990)。隨著葉輪間隙模型的引入,入口渦流計算值為0.52,得到的Q值為7600 Lbf/in時的所有密封。由于總的密封Q集中在轉子中心,所得對數衰減率值分別為:最小軸承間隙為0.17,最大軸承間隙為0.35。與I級分析一樣,II級的API穩定性驗收準則是大于0.1的對數衰減率。因此,該壓縮機在軸承間隙公差范圍內滿足API要求。

結果如表2所示,分別在圖9和圖10中給出了最小和最大軸承間隙。從圖9和圖10中也可以注意到零對數衰減率時的Q值,Q0。這些分別為22500和40000lbf/in的最小和最大軸承間隙。顯然,使用改進的Alford力預測的穩定性水平較為保守。



密封入口渦流效應
入口渦流對總密封Q的影響如圖11所示。在圖12中給出了相應的穩定性影響。需要注意的是,在最小軸承和密封間隙下,入口渦流值為0.3時,對數衰減率將提高到提高0.28。(Childs and Ramsey, 1991;Moore and Hill, 2000)


密封間隙效應
密封間隙對Q的影響如圖13所示。加工直徑公差范圍為16~20mils。假設由于葉輪的離心膨脹,最小直徑密封間隙減小4mils,圖13也給出了直徑為12mils的最小工作間隙。圖14中給出了入口渦流為0.6和最小軸承間隙時對穩定性的影響作用。


圖15說明了收斂和發散型密封間隙對穩定性的影響。假設所有密封齒均為12mils的直徑間隙,得到的對數衰減率為0.6。如果間隙從密封入口(直徑為16mils)收斂到出口(直徑為8mils),那么對數衰減率將減小到-0.11。反之,從入口(直徑為8mils)到出口(直徑為16mils),那么對數衰減率為0.23。這些計算值的前提條件是:假定最小軸承間隙,并且入口渦流值為0.6。

顯然,應該優選發散型的間隙分布,以提高穩定性。對發散型間隙而言,雖然密封主剛度為負,這種影響是最小的。此外,對于發散型間隙情況,泄漏量實際上比恒定間隙減小了。對于這種壓縮機,從密封出口位置增加到密封入口位置,葉輪隨轉速的增大而變化,從而產生不同的密封間隙。
對于發散間隙,這種影響是最小的。此外,泄漏量實際上比恒定間隙減小了發散間隙情況。對于這種壓縮機,葉輪的增長速度從眼睛密封排放位置(葉輪眼)增加到眼睛密封入口位置,從而產生不同的密封間隙。
平衡活塞蜂窩密封
堵塞與入口渦流效應
蜂窩密封的一個問題是蜂窩孔可能堵塞或填充多余物。其它非迷宮式密封也可能存在堵塞,例如孔型密封件。
蜂窩密封的這種堵塞孔效應如圖16所示,圖中給出了最小軸承間隙,以及三個不同的蜂窩密封入口渦流值:0.8,一個較糟糕的值;0.6,一個更現實的值;和0.3,模擬包含渦流制動器。結果表明,隨著蜂窩孔的填充或堵塞,穩定性降低。對于入口渦流為0.6的情況,只要有小于48%的孔隙填充,則對數衰減率就會大于0.1,滿足API要求。對于包含渦流制動器(入口渦流為0.3),只要孔隙填充數少于60%,對數衰減率就大于0.1。

例2:65000 馬力,3級丙烷制冷壓縮機
第二個例子是用于制冷的三級、三段65000 馬力丙烷壓縮機,其具有230inch的軸承跨度和Lb/Dms=10.3。轉子的重量超過36000磅,工作轉速3000rpm,采用干氣密封和五瓦塊可傾瓦滑動軸承(表1)。入口壓力為20 psi,出口壓力為100 psi,氣體摩爾重量為44。大型制冷壓縮機的典型特征是具有較低的對數衰減率和相對較小的不穩定力表現。這臺機器也不例外。該壓縮機的基本對數衰減率(僅就轉子和軸承而言,Q=0)在軸承公差范圍內分布于0.18到0.13不等。
過去對具有多過程段的壓縮機,在考慮“Wachel”型方程(Wachel和Von Nimz,1981)時,出現了適用性問題。在大多數情況下,通過逐級應用修正的Alford方程,已經解決了這些問題。在該應用中,每級表示一個過程段,該過程段內將側流添加到主流中,這發生在第二葉輪和第三葉輪之前。圖17給出了壓縮機的轉子動力學模型。


應用公式(3),可以計算預期的不穩定力Qa,總預期的失穩力Qa為23046 lbf/in。將這應用于轉子中心,分別得到最小和最大軸承剛度的對數衰減率為0.15和0.09。圖18顯示了穩定性靈敏度曲線。(軸承間隙和油入口溫度的公差范圍限定了軸承剛度的范圍)。根據API的要求,由于最壞情況δa<0.1,用Kirk(1990)開發的方法進行二級分析,以預測葉輪迷宮式密封件的性能。這些不穩定力被施加在密封的實際位置上。對于相同范圍內的軸承剛度,對數衰減率是針對以下條件計算的:
僅轉子和軸承
轉子、軸承和葉輪迷宮密封
轉子、軸承、葉輪迷宮密封和平衡活塞
表3包含了二級分析的結果和使用修正的Alford力對轉子穩定性的估計。正如預期的那樣,由于迷宮密封(包括平衡活塞)的激勵力很小,因此對轉子穩定性影響較小。對于這個應用,使用改進的Alford力預測的穩定性水平是保守的。

例3 30000馬力4級噴射壓縮機(略)
第四個例子是11000馬力的四級離心壓縮機,用于噴射,具有48英寸的軸承跨度,Lb/Dms=7.26。轉子重422磅,運行轉速為9900rpm,采用干氣密封和五瓦塊可傾瓦滑動軸承(表1)。入口壓力為5600 psi,出口壓力為9000 psi。
就噴射方面而言,該壓縮機被認為具有較高的排放壓力范圍和中等的功率與重量比值。在這樣的情況下,由于壓縮機中氣體的密度升高,不穩定力預計會更高。實際上,由于平均氣體密度為115 kg/m3,需要進行II級分析。如前所述,制造商保守地設計了具有較大中心軸段的壓縮機,以抵消預期的更高的不穩定力(圖19)。

這種情況下,修改后的Alford力計算值為72854lbf/in,大致等于示例3中的壓縮機。(圖20)。較高的氣體密度抵消了前面例子中較高的馬力。因此,對于這兩個例子,預期的不穩定力水平大致相同。表3包含了I級和II級分析的穩定性分析結果。與其它噴射壓縮機一樣,由于Q0<2Qa,需要進行II級分析,這表明預期的失穩力和驅動系統不穩定所需的量之間存在足夠的安全余量。

如前所述,對于兩個噴射壓縮機來說,Alford不穩定力幾乎相等。表3通過比較兩個II級分析,證實了這一事實。從基礎值到包括所有不穩定力條件,在軸承系數變化范圍內,對于第一噴射壓縮機的對數衰減率大約為-0.55和-0.40,對于第二噴射壓縮機的對數衰減率約為-0.45和-0.30。考慮到轉子和軸承幾何形狀的差異,這兩者可視為相當或一致。與前面的例子不同,平衡活塞產生了大部分的不穩定力。
由于壓縮機內氣體平均密度上升,因此需要進行II級分析。這臺壓縮機成功地通過了滿負荷試驗,沒有發生穩定性問題。
例5 混合制冷
在前三個例子中,通過比較I級和II級分析,得到了對數衰減率值,來確定修正的Alford方程的保守性。在本節中,提出了一種比較等效集中不穩定力的更直接的方法,類似于Memmott (2000)。示例3中,噴射壓縮機與較大的制冷壓縮機一起使用。93000馬力的混合制冷壓縮機(例5)具有222英寸的軸承跨度,Lb/Dms為10.2。圖21比較了這兩種壓縮機。轉子重44730磅,運行轉速為3000rpm,采用干氣密封和五瓦塊可傾瓦滑動軸承(表1)。入口壓力為60 psi,使用25MW的氣體,具有320 psi的出口壓力。

為了產生與修正的Alford方程計算等效的失穩力,使用以下關系計算每個密封件的等效交叉耦合剛度:


K和C值由迷宮密封分析(Kirk, 1990)確定,轉子中心的等效模態交叉耦合定義為:


從第一阻尼固有頻率的歸一化模態振型確定模態影響因子Mf,表征密封位置處的位移。對所有密封位置進行求和,得到交叉耦合力。這種模態交叉耦合,Qm,連同II級分析中計算的對數衰減率值一起,在最大軸承剛度的條件下,繪制在兩個壓縮機實例的穩定性靈敏度圖上。
圖22為例子3種第一種噴射壓縮機的結果。


該壓縮機的最小模態系數僅為0.91,反映了壓縮機的軸具有較好的剛性工作條件(stiffer shaft operation)。考慮到迷宮密封和平衡活塞力,計算模態交叉耦合系數為44933lbf/in。表3中,包括所有不穩定力的II級對數衰減率,在最大支承剛度時,為0.48。在靈敏度圖上繪制這一點,人們發現該點幾乎直接位于通過在轉子中心放置不同量值的交叉耦合剛度而得到的直線上。需要強調的是,對數衰減率繪制的δm是由II級分析計算得到的,考慮位于實際位置的密封效應。從這一點可以得出如下結論:
modal reduction產生的交叉耦合力直接與修正Alford力相媲美。
模態交叉耦合還提供了基于實際密封系數的轉子裕度指示。(在這種情況下,將44933 lbf/in與95300lbf/in的Q0量進行比較。大約存在兩倍安全余量,或更簡單地說,迷宮密封的不穩定效應可能比預測不穩定條件之前的計算值大兩倍。
對混合制冷壓縮機進行重復計算(例5)。對于這種壓縮機,最小模態系數為0.56,表示軸具有更靈活的彎曲模態。在II級分析中包括兩種密封結構,一種具有分流的平衡活塞另一種是沒有分流的密封。模態交叉耦合和最終II級對數衰減率值繪制如圖23所示。與噴射壓縮機一樣,這兩個點與I級分析的靈敏度線密切相關。這是真實的情況,即使在分流平衡活塞的情況下,凈交叉耦合項為負(或穩定)。
結論
開展了API水平I級修正的Alford交叉耦合力的計算,并證實了壓縮機的不穩定力是一種保守估計。研究了幾個工業領域的應用,包括氫壓縮機、兩個高壓噴射壓縮機、一個具有高功率與重量比的壓縮機,以及兩個大型制冷壓縮機,包括多級結構。在所有情況下,修正的Alford力,將產生最差的穩定性水平。
此外,檢查了II級分析的細節,以確定哪些參數是確定離心壓縮機穩定性的關鍵。一些已知的影響,包括軸承間隙公差和迷宮密封入口渦流,顯示出對10級氫氣壓縮機的穩定性水平有重大影響。在恒定的入口渦流為0.6的情況下,僅僅將在葉輪密封處的齒隙傾斜從8 mils 徑向收斂區變為8 mils徑向發散區,預測的對數衰減率將從-0.11變為0.23。這為提高離心式離心壓縮機的穩定性提供了另一個簡單的途徑。
最后,提出了一種模態方法來直接比較I級和II級不穩定力。除了確認修正的Alford力的保守性外,模態方法還允許使用穩定性靈敏度曲線來逼近迷宮密封系數相對于零對數衰減率閾值的安全裕度。
參數如下:
Cs=Seal diametral clearance (mils)
C=Principle damping (lbf-sec/in)
Dc=Impeller diameter (inch)
Dms=Midshaft diameter (inch)
Hc=Minimum width of the impeller or discharge volute (inch)
hp=Horsepower (hp)
k=Cross-coupled stiffness (lbf/in)
Lb=Bearing span, (inch)
Mf=Modal influence factor
N=Speed (rpm)
Nd=Damped natural frequency (cpm)
Pdisch=Discharge pressure (psi)
Pin=Inlet pressure (psi)
Q=Aerodynamic cross-coupling (lbf/in)
Qa=Anticipated aerodynamic cross-coupling (lbf/in)
Qeq=Equivalent cross-coupling (lbf/in)
Qm=Modal cross-coupling (lbf/in)
Q0=Aerodynamic cross-coupling for zero log dec (lbf/in)
s=Real part of eigenvalue
X1,2=Amplitude (mils)
β=Efficiency factor δ = Log dec
δa=Log dec for Qa
δm=Final log dec from the Level II analysis
ρratio=Density ratio
ωd=Damped natural frequency (rad/sec)
ωcs=Damped first natural frequency (rad/sec)











網友評論
條評論
最新評論