【壓縮機(jī)網(wǎng)】某公司因?yàn)槭褂眯枰拥饺蝿?wù)要求開發(fā)一款轉(zhuǎn)速n=1470r/mim,z*大活塞力P=160kN,4M型基礎(chǔ)件。這對高轉(zhuǎn)速、4M型的曲軸提出更高的精度要求。
相關(guān)人員分析研究后擬利用SolidWorks進(jìn)行曲軸動平衡仿真,使曲軸達(dá)到國際標(biāo)準(zhǔn)ISO1940規(guī)定的平衡精度,并選取曲軸精度等級G6.3,依據(jù)動平衡原理(要求慣性力和慣性力矩都達(dá)到平衡),設(shè)計出基于SolidWorks的4M16曲軸動平衡仿真分析報告,并具體提出幾種分析方法,以供參考施行研究。
方法一:Simulation有限元分析法
a)夾具:在曲軸兩軸承端設(shè)置固定鉸鏈,如圖1所示。

b) 外部載荷:在旋轉(zhuǎn)軸上添加旋轉(zhuǎn)速度n=1470r/min,方向順時針(從電機(jī)端往曲軸方向看去)如圖2所示。

c) 網(wǎng)格化:對曲軸進(jìn)行網(wǎng)格化,如圖3所示。

d)運(yùn)行并顯示結(jié)果:如圖4所示。

圖中顯示兩端軸承受力情況,得出的合力即為旋轉(zhuǎn)不平衡力F1=221.09N。
方法二:Motion運(yùn)動分析法
a)新建運(yùn)動算例,將曲軸兩端設(shè)好的點(diǎn)分別與機(jī)身旋轉(zhuǎn)軸(Z軸)重合。
b)設(shè)置旋轉(zhuǎn)馬達(dá),轉(zhuǎn)速n=1470r/min,方向順時針,如圖5所示。

c)添加重力:將Y軸正向設(shè)為重力方向(因?yàn)檠芯克捷SX方向受力,可以不設(shè)置重力),如圖6所示。

d)點(diǎn)擊計算按鈕,輸出兩端支反力作用曲線圖,如圖7所示。

e)將左右兩側(cè)支反力進(jìn)行矢量疊加,獲得的曲線圖如圖8所示。

這是一條類正余弦曲線,其極值F2=221N(在水平方向0°和180°)。
方法三:傳統(tǒng)計算法
a)原理:具有一定轉(zhuǎn)速的轉(zhuǎn)子,由于材料組織不均性、零件外形誤差、裝配誤差以及結(jié)構(gòu)形狀局部不對稱性(如鍵槽)等原因,使通過轉(zhuǎn)子重心的主慣性軸與旋轉(zhuǎn)軸線不重合,因而旋轉(zhuǎn)時,轉(zhuǎn)子產(chǎn)生不平衡離心力,其值如下式所示:
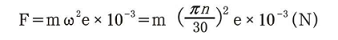
式中:m為轉(zhuǎn)子的重量(kg);ω為轉(zhuǎn)子角速度(rad/s);n為轉(zhuǎn)子速度(r/min);e為轉(zhuǎn)子重心對旋轉(zhuǎn)軸線的偏移,即偏心距(mm)。
b)由曲軸的質(zhì)量屬性可知曲軸質(zhì)量,重心位置,如圖9所示。

c)該曲軸旋轉(zhuǎn)不平衡慣性力
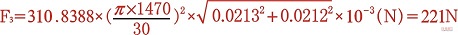
結(jié)論
從上述三種方法可知F1=F2=F3=221N,即無論使用Simulation有限元分析法還是Motion運(yùn)動分析法,其結(jié)果與傳統(tǒng)計算法得出的結(jié)果一致。
確定z*大往復(fù)質(zhì)量Mp
已知電機(jī)轉(zhuǎn)速n=1470r/mim,取綜合活塞力
P=156kN,λ=0.1724,行程S=2r=2×63.5=127mm,則往復(fù)z*大質(zhì)量Mpmax=P/[rω2(1+λ)]=88.4kg
取往復(fù)質(zhì)量Mp=85kg[相對運(yùn)動兩列的往復(fù)運(yùn)動重量誤差,不得大于1磅(0.4536 kg)]
整機(jī)進(jìn)行Motion運(yùn)動仿真
將連桿、曲軸、活塞及活塞桿等運(yùn)動件進(jìn)行裝配,在此裝配體中進(jìn)行Motion運(yùn)動仿真(具體步驟見方法二),得出軸承兩端受力曲線圖,如圖10所示。

從圖中可知,左側(cè)受力在±1.82×104 N成正余弦波動,右側(cè)受力在±1.84×104 N成正余弦波動,該力組成的力矩是機(jī)組震動的根源。這種周期性變化的支反力是由于一階慣性力矩不平衡引起的,必須予以降低甚至消除。
4M16曲軸連桿機(jī)構(gòu)受力分析
1、氣體力與摩擦力(旋轉(zhuǎn)摩擦力和往復(fù)摩擦力)屬于內(nèi)力,它們均在機(jī)器內(nèi)部相互抵消掉。
2、往復(fù)慣性力和旋轉(zhuǎn)慣性力屬于外力,它們在機(jī)器內(nèi)部若不能平衡掉,那么它們會通過主軸承和機(jī)體傳遞至機(jī)器外部來。因?yàn)槠鋽?shù)值大小和方向隨著曲柄轉(zhuǎn)角周期變化,會引起機(jī)器的振動和噪聲,縮短軸承使用壽命。
3、往復(fù)慣性力:往復(fù)慣性力的大小由往復(fù)質(zhì)量ms與其加速度a大小決定的,方向同加速度a方向,其表達(dá)式為I=msa=msω2r(cosθ+λcos2θ)
4、旋轉(zhuǎn)慣性力:是由曲柄銷質(zhì)量mr沿著旋轉(zhuǎn)軸旋轉(zhuǎn)引起的,方向始終沿著曲柄銷半徑向外, 其表達(dá)式為Ir=mrω2r
5、4M16曲軸連桿機(jī)構(gòu)簡圖如圖11所示:第1列所處位置設(shè)為曲柄轉(zhuǎn)角為0,b為相鄰列間距,L為兩端平衡重距離,δ為1、3列氣缸中心線夾角等于90°,λ為1、2列氣缸中心線夾角等于180°,其慣性力與慣性力矩如表1所示。
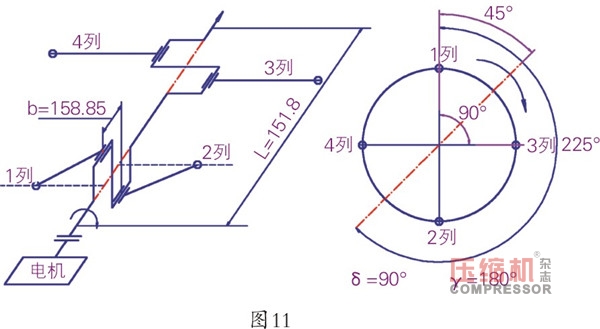
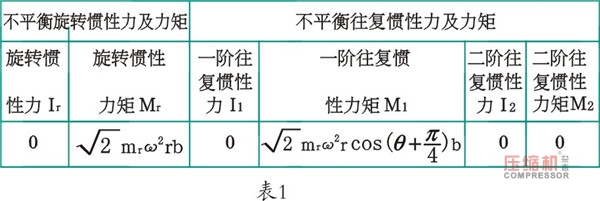
從表1中知旋轉(zhuǎn)慣性力Ir、一階往復(fù)慣性力I1、二階往復(fù)慣性力I2、二階往復(fù)慣性力矩M2均等于零;旋轉(zhuǎn)慣性力矩Mr可在曲柄銷對側(cè)加平衡重來平衡(本文曲軸的Mr已配平衡,過程不再贅述);一階往復(fù)慣性力矩 ,其極值在曲柄轉(zhuǎn)角45°和225°方向上,故在其反方向225°和45°方向上加配重塊進(jìn)行平衡。一般在曲軸兩端,因?yàn)榇藭r力臂z*大,則配置塊的質(zhì)量z*輕,對曲軸平衡性能更有利。
,其極值在曲柄轉(zhuǎn)角45°和225°方向上,故在其反方向225°和45°方向上加配重塊進(jìn)行平衡。一般在曲軸兩端,因?yàn)榇藭r力臂z*大,則配置塊的質(zhì)量z*輕,對曲軸平衡性能更有利。
6、在曲軸兩端,曲柄轉(zhuǎn)角分別為225°和45°方向加配重塊,如圖12所示。

7、將修改后的曲軸重新裝入裝配體中再進(jìn)行Motion運(yùn)動仿真(具體步驟見方案二),得出軸承兩端受力曲線圖,如圖13所示。

由曲線圖可知,左側(cè)支反力由±1.82×104N 銳減至±0.12×104N, 右側(cè)支反力由±1.84×104N 銳減至 ±0.10×104N,兩側(cè)力是大幅減低(降幅約15倍),有效抵消了反作用力矩,這對機(jī)組震動是有益的。現(xiàn)將上圖中兩側(cè)支反力進(jìn)行矢量疊加,求的合力如圖14所示。
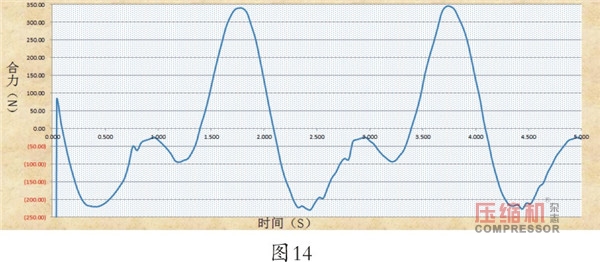
此曲線圖表示該運(yùn)動機(jī)構(gòu)在水平軸(X)方向所受的合力,大小在-250~+350(N)范圍內(nèi)波動。
8、驗(yàn)證一階慣性矩平衡情況
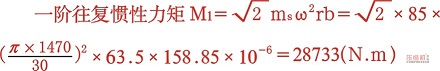
所加配重塊質(zhì)量屬性如圖15所示。


剩余不平衡力矩△M=M1-M'=400(N.m),此值相對于一階往復(fù)慣性力矩M1非常小(1.4%),可以認(rèn)為一階往復(fù)慣性力矩被配重塊構(gòu)成的反力矩平衡掉了。
1、達(dá)到的技術(shù)指標(biāo)
將修改后的曲軸(圖12)進(jìn)行Simulation有限元分析,具體步驟同方法一,分析結(jié)果如圖16所示。


2、用途及應(yīng)用范圍
基于SolidWorks的曲軸動平衡仿真可以模擬各類轉(zhuǎn)子動平衡:可適用適有轉(zhuǎn)軸或可裝配工藝軸的轉(zhuǎn)子,如壓縮機(jī)及發(fā)動機(jī)曲軸、機(jī)床主軸、滾筒、風(fēng)機(jī)、增壓器、電機(jī)轉(zhuǎn)子、汽輪機(jī)等;也適用于轉(zhuǎn)子本身不具轉(zhuǎn)軸的盤狀工件,如離合器、齒輪、風(fēng)扇、壓盤及其總成、制動盤、風(fēng)葉、水泵葉輪、汽車飛輪、剎車轂、皮帶輪、砂輪等盤類零件。
3、經(jīng)濟(jì)效益和社會效益
傳統(tǒng)硬支撐平衡機(jī)雖能較好地對轉(zhuǎn)子本身進(jìn)行平衡,但是對于轉(zhuǎn)子尺寸相差較大時,往往需要不同規(guī)格尺寸的動平衡機(jī),而且試驗(yàn)時仍需將轉(zhuǎn)子從機(jī)器上拆下來,這樣明顯是既不經(jīng)濟(jì),也十分費(fèi)工。當(dāng)對曲軸連桿這類特殊轉(zhuǎn)子進(jìn)行平衡時需要折算連桿作旋轉(zhuǎn)運(yùn)動質(zhì)量,一般很難保證精度。
基于SolidWorks的曲軸動平衡仿真則完全可以模擬曲軸運(yùn)動件受力情況并得出受力曲線圖,數(shù)據(jù)更準(zhǔn)確,而且操作簡單。這種方法在曲軸設(shè)計前期就可以對曲軸進(jìn)行動平衡分析,提高曲軸設(shè)計精度、縮短曲軸開發(fā)時間、降低開發(fā)成本。尤其對于高速往復(fù)式壓縮機(jī),不僅可以平衡力,而且還可以平衡力矩,確保高速往復(fù)式壓縮機(jī)運(yùn)行平穩(wěn),減少軸承磨損,降低噪聲。
作者簡介:
王孝磊(1986-),男,大學(xué)本科,安瑞科(蚌埠)壓縮機(jī)有限公司研發(fā)室。
【壓縮機(jī)網(wǎng)】某公司因?yàn)槭褂眯枰拥饺蝿?wù)要求開發(fā)一款轉(zhuǎn)速n=1470r/mim,z*大活塞力P=160kN,4M型基礎(chǔ)件。這對高轉(zhuǎn)速、4M型的曲軸提出更高的精度要求。
相關(guān)人員分析研究后擬利用SolidWorks進(jìn)行曲軸動平衡仿真,使曲軸達(dá)到國際標(biāo)準(zhǔn)ISO1940規(guī)定的平衡精度,并選取曲軸精度等級G6.3,依據(jù)動平衡原理(要求慣性力和慣性力矩都達(dá)到平衡),設(shè)計出基于SolidWorks的4M16曲軸動平衡仿真分析報告,并具體提出幾種分析方法,以供參考施行研究。
方法一:Simulation有限元分析法
a)夾具:在曲軸兩軸承端設(shè)置固定鉸鏈,如圖1所示。

b) 外部載荷:在旋轉(zhuǎn)軸上添加旋轉(zhuǎn)速度n=1470r/min,方向順時針(從電機(jī)端往曲軸方向看去)如圖2所示。

c) 網(wǎng)格化:對曲軸進(jìn)行網(wǎng)格化,如圖3所示。

d)運(yùn)行并顯示結(jié)果:如圖4所示。

圖中顯示兩端軸承受力情況,得出的合力即為旋轉(zhuǎn)不平衡力F1=221.09N。
方法二:Motion運(yùn)動分析法
a)新建運(yùn)動算例,將曲軸兩端設(shè)好的點(diǎn)分別與機(jī)身旋轉(zhuǎn)軸(Z軸)重合。
b)設(shè)置旋轉(zhuǎn)馬達(dá),轉(zhuǎn)速n=1470r/min,方向順時針,如圖5所示。

c)添加重力:將Y軸正向設(shè)為重力方向(因?yàn)檠芯克捷SX方向受力,可以不設(shè)置重力),如圖6所示。

d)點(diǎn)擊計算按鈕,輸出兩端支反力作用曲線圖,如圖7所示。

e)將左右兩側(cè)支反力進(jìn)行矢量疊加,獲得的曲線圖如圖8所示。

這是一條類正余弦曲線,其極值F2=221N(在水平方向0°和180°)。
方法三:傳統(tǒng)計算法
a)原理:具有一定轉(zhuǎn)速的轉(zhuǎn)子,由于材料組織不均性、零件外形誤差、裝配誤差以及結(jié)構(gòu)形狀局部不對稱性(如鍵槽)等原因,使通過轉(zhuǎn)子重心的主慣性軸與旋轉(zhuǎn)軸線不重合,因而旋轉(zhuǎn)時,轉(zhuǎn)子產(chǎn)生不平衡離心力,其值如下式所示:
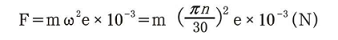
式中:m為轉(zhuǎn)子的重量(kg);ω為轉(zhuǎn)子角速度(rad/s);n為轉(zhuǎn)子速度(r/min);e為轉(zhuǎn)子重心對旋轉(zhuǎn)軸線的偏移,即偏心距(mm)。
b)由曲軸的質(zhì)量屬性可知曲軸質(zhì)量,重心位置,如圖9所示。

c)該曲軸旋轉(zhuǎn)不平衡慣性力
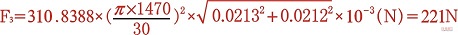
結(jié)論
從上述三種方法可知F1=F2=F3=221N,即無論使用Simulation有限元分析法還是Motion運(yùn)動分析法,其結(jié)果與傳統(tǒng)計算法得出的結(jié)果一致。
確定z*大往復(fù)質(zhì)量Mp
已知電機(jī)轉(zhuǎn)速n=1470r/mim,取綜合活塞力
P=156kN,λ=0.1724,行程S=2r=2×63.5=127mm,則往復(fù)z*大質(zhì)量Mpmax=P/[rω2(1+λ)]=88.4kg
取往復(fù)質(zhì)量Mp=85kg[相對運(yùn)動兩列的往復(fù)運(yùn)動重量誤差,不得大于1磅(0.4536 kg)]
整機(jī)進(jìn)行Motion運(yùn)動仿真
將連桿、曲軸、活塞及活塞桿等運(yùn)動件進(jìn)行裝配,在此裝配體中進(jìn)行Motion運(yùn)動仿真(具體步驟見方法二),得出軸承兩端受力曲線圖,如圖10所示。

從圖中可知,左側(cè)受力在±1.82×104 N成正余弦波動,右側(cè)受力在±1.84×104 N成正余弦波動,該力組成的力矩是機(jī)組震動的根源。這種周期性變化的支反力是由于一階慣性力矩不平衡引起的,必須予以降低甚至消除。
4M16曲軸連桿機(jī)構(gòu)受力分析
1、氣體力與摩擦力(旋轉(zhuǎn)摩擦力和往復(fù)摩擦力)屬于內(nèi)力,它們均在機(jī)器內(nèi)部相互抵消掉。
2、往復(fù)慣性力和旋轉(zhuǎn)慣性力屬于外力,它們在機(jī)器內(nèi)部若不能平衡掉,那么它們會通過主軸承和機(jī)體傳遞至機(jī)器外部來。因?yàn)槠鋽?shù)值大小和方向隨著曲柄轉(zhuǎn)角周期變化,會引起機(jī)器的振動和噪聲,縮短軸承使用壽命。
3、往復(fù)慣性力:往復(fù)慣性力的大小由往復(fù)質(zhì)量ms與其加速度a大小決定的,方向同加速度a方向,其表達(dá)式為I=msa=msω2r(cosθ+λcos2θ)
4、旋轉(zhuǎn)慣性力:是由曲柄銷質(zhì)量mr沿著旋轉(zhuǎn)軸旋轉(zhuǎn)引起的,方向始終沿著曲柄銷半徑向外, 其表達(dá)式為Ir=mrω2r
5、4M16曲軸連桿機(jī)構(gòu)簡圖如圖11所示:第1列所處位置設(shè)為曲柄轉(zhuǎn)角為0,b為相鄰列間距,L為兩端平衡重距離,δ為1、3列氣缸中心線夾角等于90°,λ為1、2列氣缸中心線夾角等于180°,其慣性力與慣性力矩如表1所示。


從表1中知旋轉(zhuǎn)慣性力Ir、一階往復(fù)慣性力I1、二階往復(fù)慣性力I2、二階往復(fù)慣性力矩M2均等于零;旋轉(zhuǎn)慣性力矩Mr可在曲柄銷對側(cè)加平衡重來平衡(本文曲軸的Mr已配平衡,過程不再贅述);一階往復(fù)慣性力矩 ,其極值在曲柄轉(zhuǎn)角45°和225°方向上,故在其反方向225°和45°方向上加配重塊進(jìn)行平衡。一般在曲軸兩端,因?yàn)榇藭r力臂z*大,則配置塊的質(zhì)量z*輕,對曲軸平衡性能更有利。
,其極值在曲柄轉(zhuǎn)角45°和225°方向上,故在其反方向225°和45°方向上加配重塊進(jìn)行平衡。一般在曲軸兩端,因?yàn)榇藭r力臂z*大,則配置塊的質(zhì)量z*輕,對曲軸平衡性能更有利。
 ,其極值在曲柄轉(zhuǎn)角45°和225°方向上,故在其反方向225°和45°方向上加配重塊進(jìn)行平衡。一般在曲軸兩端,因?yàn)榇藭r力臂z*大,則配置塊的質(zhì)量z*輕,對曲軸平衡性能更有利。
,其極值在曲柄轉(zhuǎn)角45°和225°方向上,故在其反方向225°和45°方向上加配重塊進(jìn)行平衡。一般在曲軸兩端,因?yàn)榇藭r力臂z*大,則配置塊的質(zhì)量z*輕,對曲軸平衡性能更有利。 6、在曲軸兩端,曲柄轉(zhuǎn)角分別為225°和45°方向加配重塊,如圖12所示。

7、將修改后的曲軸重新裝入裝配體中再進(jìn)行Motion運(yùn)動仿真(具體步驟見方案二),得出軸承兩端受力曲線圖,如圖13所示。

由曲線圖可知,左側(cè)支反力由±1.82×104N 銳減至±0.12×104N, 右側(cè)支反力由±1.84×104N 銳減至 ±0.10×104N,兩側(cè)力是大幅減低(降幅約15倍),有效抵消了反作用力矩,這對機(jī)組震動是有益的。現(xiàn)將上圖中兩側(cè)支反力進(jìn)行矢量疊加,求的合力如圖14所示。

此曲線圖表示該運(yùn)動機(jī)構(gòu)在水平軸(X)方向所受的合力,大小在-250~+350(N)范圍內(nèi)波動。
8、驗(yàn)證一階慣性矩平衡情況
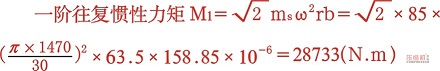
所加配重塊質(zhì)量屬性如圖15所示。


剩余不平衡力矩△M=M1-M'=400(N.m),此值相對于一階往復(fù)慣性力矩M1非常小(1.4%),可以認(rèn)為一階往復(fù)慣性力矩被配重塊構(gòu)成的反力矩平衡掉了。
1、達(dá)到的技術(shù)指標(biāo)
將修改后的曲軸(圖12)進(jìn)行Simulation有限元分析,具體步驟同方法一,分析結(jié)果如圖16所示。


2、用途及應(yīng)用范圍
基于SolidWorks的曲軸動平衡仿真可以模擬各類轉(zhuǎn)子動平衡:可適用適有轉(zhuǎn)軸或可裝配工藝軸的轉(zhuǎn)子,如壓縮機(jī)及發(fā)動機(jī)曲軸、機(jī)床主軸、滾筒、風(fēng)機(jī)、增壓器、電機(jī)轉(zhuǎn)子、汽輪機(jī)等;也適用于轉(zhuǎn)子本身不具轉(zhuǎn)軸的盤狀工件,如離合器、齒輪、風(fēng)扇、壓盤及其總成、制動盤、風(fēng)葉、水泵葉輪、汽車飛輪、剎車轂、皮帶輪、砂輪等盤類零件。
3、經(jīng)濟(jì)效益和社會效益
傳統(tǒng)硬支撐平衡機(jī)雖能較好地對轉(zhuǎn)子本身進(jìn)行平衡,但是對于轉(zhuǎn)子尺寸相差較大時,往往需要不同規(guī)格尺寸的動平衡機(jī),而且試驗(yàn)時仍需將轉(zhuǎn)子從機(jī)器上拆下來,這樣明顯是既不經(jīng)濟(jì),也十分費(fèi)工。當(dāng)對曲軸連桿這類特殊轉(zhuǎn)子進(jìn)行平衡時需要折算連桿作旋轉(zhuǎn)運(yùn)動質(zhì)量,一般很難保證精度。
基于SolidWorks的曲軸動平衡仿真則完全可以模擬曲軸運(yùn)動件受力情況并得出受力曲線圖,數(shù)據(jù)更準(zhǔn)確,而且操作簡單。這種方法在曲軸設(shè)計前期就可以對曲軸進(jìn)行動平衡分析,提高曲軸設(shè)計精度、縮短曲軸開發(fā)時間、降低開發(fā)成本。尤其對于高速往復(fù)式壓縮機(jī),不僅可以平衡力,而且還可以平衡力矩,確保高速往復(fù)式壓縮機(jī)運(yùn)行平穩(wěn),減少軸承磨損,降低噪聲。
作者簡介:
王孝磊(1986-),男,大學(xué)本科,安瑞科(蚌埠)壓縮機(jī)有限公司研發(fā)室。











網(wǎng)友評論
條評論
最新評論